Løs ligningene: a) sinx=1/2, x∈[0,2π) b) 2cos(2x)=√2, x∈[0°,180°) c) √3 tanx-3=0, x∈R d) 2sin²x+5sinx=3, x∈[-180°,180°)
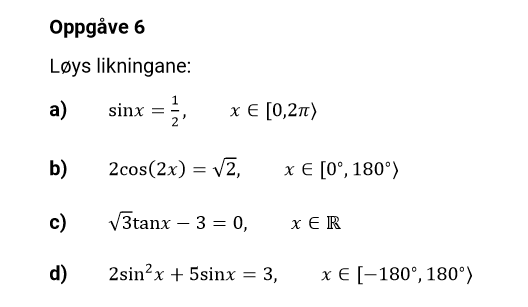
Understand the Problem
Spørsmålet ber oss om å løse fire trigonometriske ligninger over gitte intervaller. Hver ligning involverer sinus, cosinus og tangent funksjoner, og vi må finne verdier av x som tilfredsstiller disse ligningene.
Answer
a) \( x = \frac{\pi}{6}, \; \frac{5\pi}{6} \) b) \( x = \frac{\pi}{8}, \; \frac{7\pi}{8} \) c) \( x = \frac{\pi}{3} + n\pi, \; n \in \mathbb{Z} \) d) \( x = \frac{\pi}{6}, \; \frac{5\pi}{6} \)
Answer for screen readers
a) ( x = \frac{\pi}{6}, ; \frac{5\pi}{6} )
b) ( x = \frac{\pi}{8}, ; \frac{7\pi}{8} )
c) ( x = \frac{\pi}{3} + n\pi, ; n \in \mathbb{Z} )
d) ( x = \frac{\pi}{6}, ; \frac{5\pi}{6} )
Steps to Solve
- Løsning av a) ( \sin x = \frac{1}{2} )
Vi vet at ( \sin x = \frac{1}{2} ) har løsninger ved ( x = \frac{\pi}{6} ) og ( x = \frac{5\pi}{6} ) innenfor intervallet ( [0, 2\pi] ).
- Løsning av b) ( 2\cos(2x) = \sqrt{2} )
Først deler vi begge sider med 2: $$ \cos(2x) = \frac{\sqrt{2}}{2} $$ Dette gir oss løsninger ( 2x = \frac{\pi}{4} ) og ( 2x = \frac{7\pi}{4} ). Deretter deler vi med 2 for å finne ( x ): $$ x = \frac{\pi}{8} \quad \text{og} \quad x = \frac{7\pi}{8} $$
- Løsning av c) ( \sqrt{3}\tan x - 3 = 0 )
Vi begynner med å isolere tan: $$ \sqrt{3}\tan x = 3 $$ Så deler vi begge sider med ( \sqrt{3} ): $$ \tan x = \sqrt{3} $$ Dette gir løsninger ( x = \frac{\pi}{3} + n\pi ) for ( n \in \mathbb{Z} ).
- Løsning av d) ( 2\sin^2 x + 5\sin x - 3 = 0 )
Dette er en kvadratisk ligning i ( \sin x ). La ( y = \sin x ): $$ 2y^2 + 5y - 3 = 0 $$ Bruker kvadratisk formel: $$ y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$ Her er ( a = 2, b = 5, c = -3 ): $$ y = \frac{-5 \pm \sqrt{5^2 - 4\cdot2\cdot(-3)}}{2\cdot2} = \frac{-5 \pm \sqrt{25 + 24}}{4} = \frac{-5 \pm 7}{4} $$ Dette gir oss ( y = \frac{1}{2} ) og ( y = -3 ) (ignoreres da ( \sin x ) må være mellom -1 og 1). Da har vi ( \sin x = \frac{1}{2} ).
- Finne ( x )
Fra tidligere punkt vet vi at ( \sin x = \frac{1}{2} ) gir ( x = \frac{\pi}{6} ) og ( x = \frac{5\pi}{6} ).
a) ( x = \frac{\pi}{6}, ; \frac{5\pi}{6} )
b) ( x = \frac{\pi}{8}, ; \frac{7\pi}{8} )
c) ( x = \frac{\pi}{3} + n\pi, ; n \in \mathbb{Z} )
d) ( x = \frac{\pi}{6}, ; \frac{5\pi}{6} )
More Information
Disse løsningene er basert på kjennskap til de trigonometriske funksjonene og deres indikatoriske verdier. For sinus og cosinus, brukte vi kjente vinkler, mens for tangens benyttet vi dens definisjon. Den kvadratiske ligningen ble løst med den generelle formelen.
Tips
- Glemming av det faktum at trigonometriske funksjoner er periodiske og kan ha flere løsninger.
- Feil ved håndtering av kvadratiske ligninger, spesielt med fortegn.
- Å anta at alle løsninger ligger innenfor de gitte intervallene uten å kontrollere.
AI-generated content may contain errors. Please verify critical information