Look at the following piecewise function. Use the expression evaluator to write the correct equation.
Understand the Problem
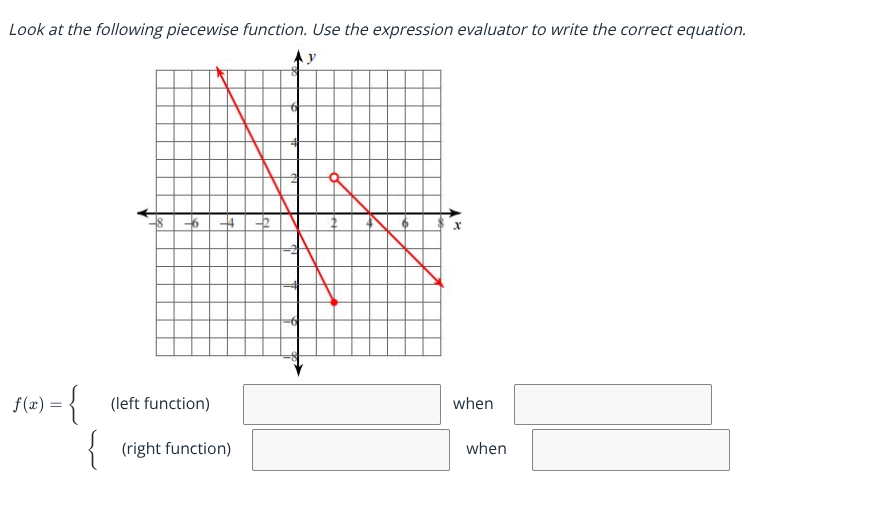
The question is asking to analyze a piecewise function displayed in a graph and then to fill in the appropriate equations that correspond to the left and right sections of the graph based on their intervals.
Answer
$$ f(x) = \begin{cases} -\frac{2}{5}x + \frac{4}{5} & \text{when } x \leq 2 \\ -x + 2 & \text{when } x > 2 \end{cases} $$
Answer for screen readers
$$ f(x) = \begin{cases} -\frac{2}{5}x + \frac{4}{5} & \text{when } x \leq 2 \ -x + 2 & \text{when } x > 2 \end{cases} $$
Steps to Solve
-
Identify the left function The left part of the graph stretches from $x = -8$ to $x = 2$. It's a line with a downward slope. We can find the equation of this line using two points: at $(-8, 4)$ and $(2, 0)$.
-
Calculate the slope ( m ): $$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{0 - 4}{2 - (-8)} = \frac{-4}{10} = -\frac{2}{5} $$
-
Use the point-slope form ( y - y_1 = m(x - x_1) ). Using point $(2, 0)$: $$ y - 0 = -\frac{2}{5}(x - 2) $$ Simplifying gives: $$ y = -\frac{2}{5}x + \frac{4}{5} $$
-
-
State the domain for the left function The left function is defined for the interval $x \leq 2$.
-
Identify the right function The right part of the graph stretches from $x = 2$ to $x = 6$. It's another line with a different slope. The two points we can use are $(2, 0)$ and $(6, -4)$.
-
Calculate the slope ( m ): $$ m = \frac{-4 - 0}{6 - 2} = \frac{-4}{4} = -1 $$
-
Using point-slope form with point $(2, 0)$: $$ y - 0 = -1(x - 2) $$ Simplifying gives: $$ y = -x + 2 $$
-
-
State the domain for the right function The right function is defined for the interval $x > 2$.
$$ f(x) = \begin{cases} -\frac{2}{5}x + \frac{4}{5} & \text{when } x \leq 2 \ -x + 2 & \text{when } x > 2 \end{cases} $$
More Information
This piecewise function describes two linear sections. The left function has a negative slope, indicating it decreases, while the right function has a steeper slope, indicating a quicker decrease.
Tips
- Using incorrect points for calculating the slope can lead to wrong equations.
- Forgetting to set appropriate intervals for the piecewise function.
- Failing to simplify the equations properly.
AI-generated content may contain errors. Please verify critical information