lim (1 - sin x) / (cos x) as x approaches π/2
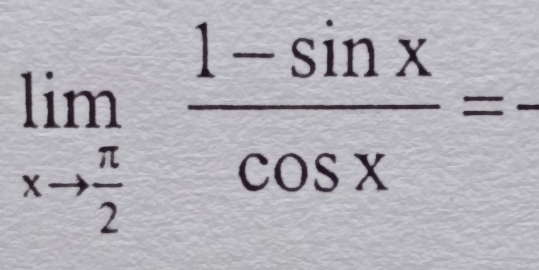
Understand the Problem
The question is asking to evaluate a limit expression involving trigonometric functions as x approaches π/2. It involves simplifying the expression and applying limit techniques.
Answer
The limit is $0$.
Answer for screen readers
The limit is $0$.
Steps to Solve
-
Substituting the limit directly Start by substituting $x = \frac{\pi}{2}$ into the limit expression: $$ \lim_{x \to \frac{\pi}{2}} \frac{1 - \sin x}{\cos x} $$ This gives: $$ \frac{1 - \sin \frac{\pi}{2}}{\cos \frac{\pi}{2}} = \frac{1 - 1}{0} = \frac{0}{0} $$ This is an indeterminate form.
-
Applying L'Hôpital's Rule Since we encountered the $ \frac{0}{0} $ indeterminate form, we can apply L'Hôpital's Rule. Take the derivative of the numerator and the denominator:
- Derivative of the numerator: $\frac{d}{dx}(1 - \sin x) = -\cos x$
- Derivative of the denominator: $\frac{d}{dx}(\cos x) = -\sin x$
Thus, we rewrite the limit: $$ \lim_{x \to \frac{\pi}{2}} \frac{-\cos x}{-\sin x} \implies \lim_{x \to \frac{\pi}{2}} \frac{\cos x}{\sin x} $$
- Evaluating the new limit Now substitute $x = \frac{\pi}{2}$ into the new expression: $$ \frac{\cos \frac{\pi}{2}}{\sin \frac{\pi}{2}} = \frac{0}{1} = 0 $$
The limit is $0$.
More Information
The limit evaluated to 0, which indicates that as $x$ approaches $\frac{\pi}{2}$, the expression becomes close to zero. L'Hôpital's Rule is a powerful technique used to deal with indeterminate forms like $ \frac{0}{0} $.
Tips
- Not recognizing the indeterminate form: Before applying L'Hôpital's Rule, always check if the limit results in an indeterminate form.
- Miscalculating derivatives: Ensure accurate differentiation of both the numerator and denominator.
AI-generated content may contain errors. Please verify critical information