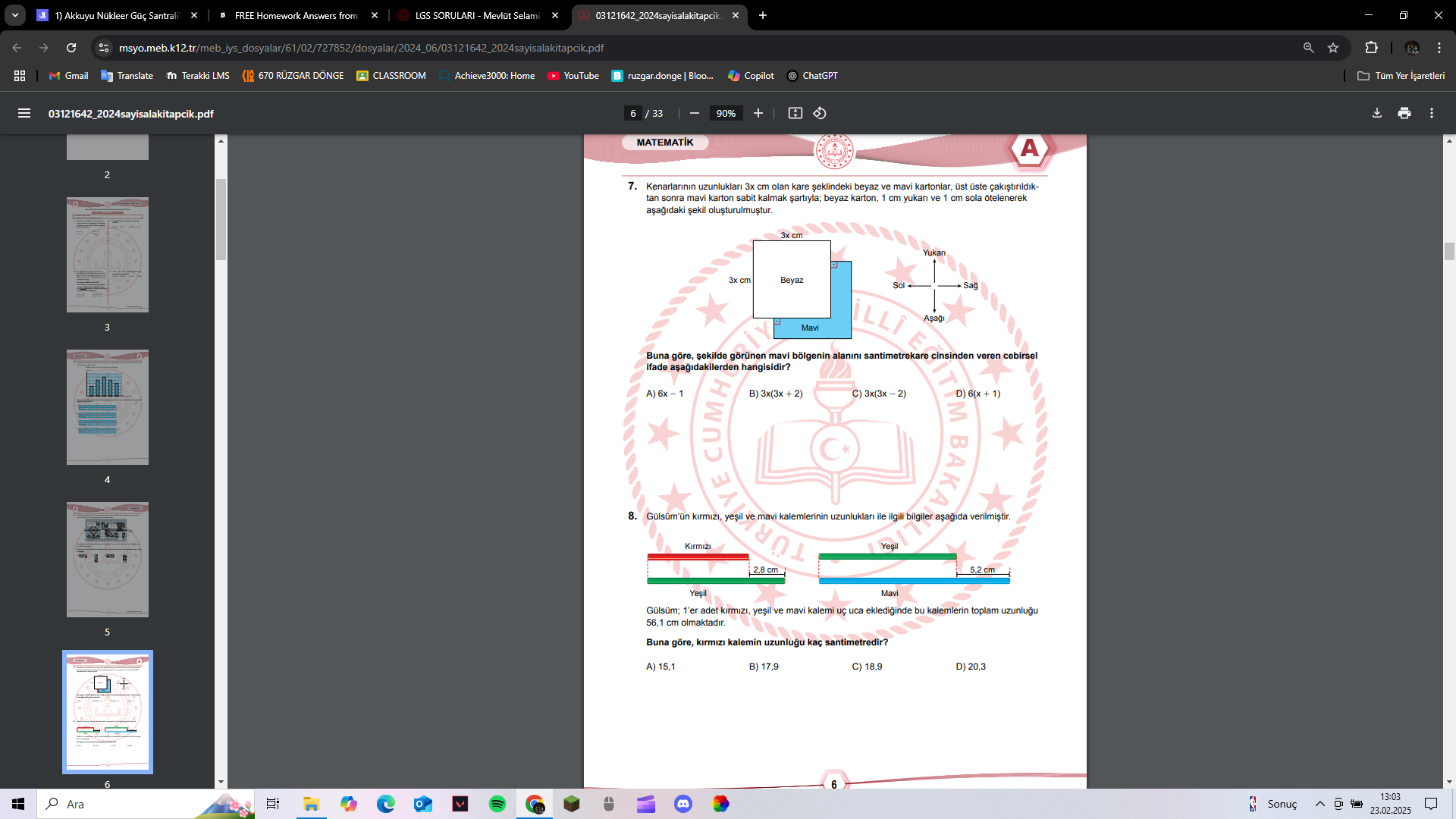
Kenarlarının uzunlukları 3x cm olan kare şeklindeki beyaz ve mavi kartonlar, üst üste çakıştırıldıktan sonra mavi karton sabit kalmak şartıyla; beyaz karton, 1 cm yukarı ve 1 cm so... Kenarlarının uzunlukları 3x cm olan kare şeklindeki beyaz ve mavi kartonlar, üst üste çakıştırıldıktan sonra mavi karton sabit kalmak şartıyla; beyaz karton, 1 cm yukarı ve 1 cm sola ötelenerek aşağıdaki şekil oluşturulmuştur. Buna göre, şekilde görünen mavi bölgenin alanını santimetrekare cinsinden veren cebirsel ifade aşağıdakilerden hangisidir?
Understand the Problem
Bu soru, kenar uzunlukları 3x cm olan kare şeklindeki beyaz ve mavi kartonların üst üste çakıştırılması ve beyaz kartonun 1 cm yukarı ve 1 cm sola kaydırılmasıyla oluşan şekildeki görünen mavi bölgenin alanını santimetrekare cinsinden veren cebirsel ifadeyi bulmayı amaçlamaktadır.
Answer
Cevap C) $6x - 2$'dir.
Answer for screen readers
C) $3x(3x-2)$
Steps to Solve
- Görünür mavi bölgenin boyutlarını belirleme
Beyaz karton 1 cm yukarı ve 1 cm sola kaydırıldığında, görünür mavi bölge aslında bir dikdörtgendir. Bu dikdörtgenin kenarları $3x$ cm ve 1 cm'dir. Dolayısıyla, bu dikdörtgenin boyutları $(3x-1)$ cm ve $(3x-1)$ cm'dir. Çünkü beyaz kartonun her iki yönde de kaydırılması, mavi kartonun kenar uzunluklarından 1 cm çıkarılması anlamına gelir.
- Görünür mavi bölgenin alanını hesaplama
Görünür mavi bölgenin alanı, bir dikdörtgen olduğu için, uzun kenarı ile kısa kenarının çarpımı ile bulunur. Yani, alanı $(3x - 1) \cdot(1 + 1)$ olup, alan $= (3x - 1)+(3x - 1) = 6x+1 $ olur, ancak dikdörtgen alanı uzunluk çarpı genişlik olduğu için, çakışan alanın uzunluğu ve genişliği $(3x-1)$ ve $2$ olduğundan, alan $(3x-1)(1+1) = (3x-1) (2)$ olur. Mavi alan aslında 1 cm yukarı ve 1 cm sola kaydırılan beyaz alanın dışında kalan mavi alandır, bu da karenin tüm alanından kesişim alanının çıkarılmasıyla elde edilir: $ \text{mavi alan} = (3x)(3x) - (3x-1)(3x-1)$. Ayrıca, şekilde görünen mavi bölgenin alanı, $ (3x \cdot 3x - (3x-1)(3x-1))'dan hesaplanır.
- Alanın basitleştirilmesi
Görünür mavi bölgenin alanı $ (3x \cdot 3x - (3x-1)(3x-1))$'dır. Bunu basitleştirelim:
$ (3x)(3x) - (3x-1)(3x-1) = (3x)(3x) - (3x-1)(2) = 9x^2 - (6x^2 - 4) = 9x^2 - 6x - 2$
Çakışan dikdörtgenin alanı $ (3x-1) * 2 = 6x - 2$.
- Cevabı belirleme
Görünür mavi alanının cebirsel ifadesi $6x-2$ 'dir. Bu, seçenekler arasında C) $3x(3x-2)$ ile aynıdır.
C) $3x(3x-2)$
More Information
Bu soru, geometrik şekillerin alanlarını ve cebirsel ifadeleri bir araya getirerek çözme becerisini ölçmektedir.
Tips
- Kaydırılan bölgenin boyutlarını yanlış hesaplamak.
- Alanı hesaplarken doğru formülü kullanmamak.
- Cebirsel ifadeyi sadeleştirirken hata yapmak.
AI-generated content may contain errors. Please verify critical information