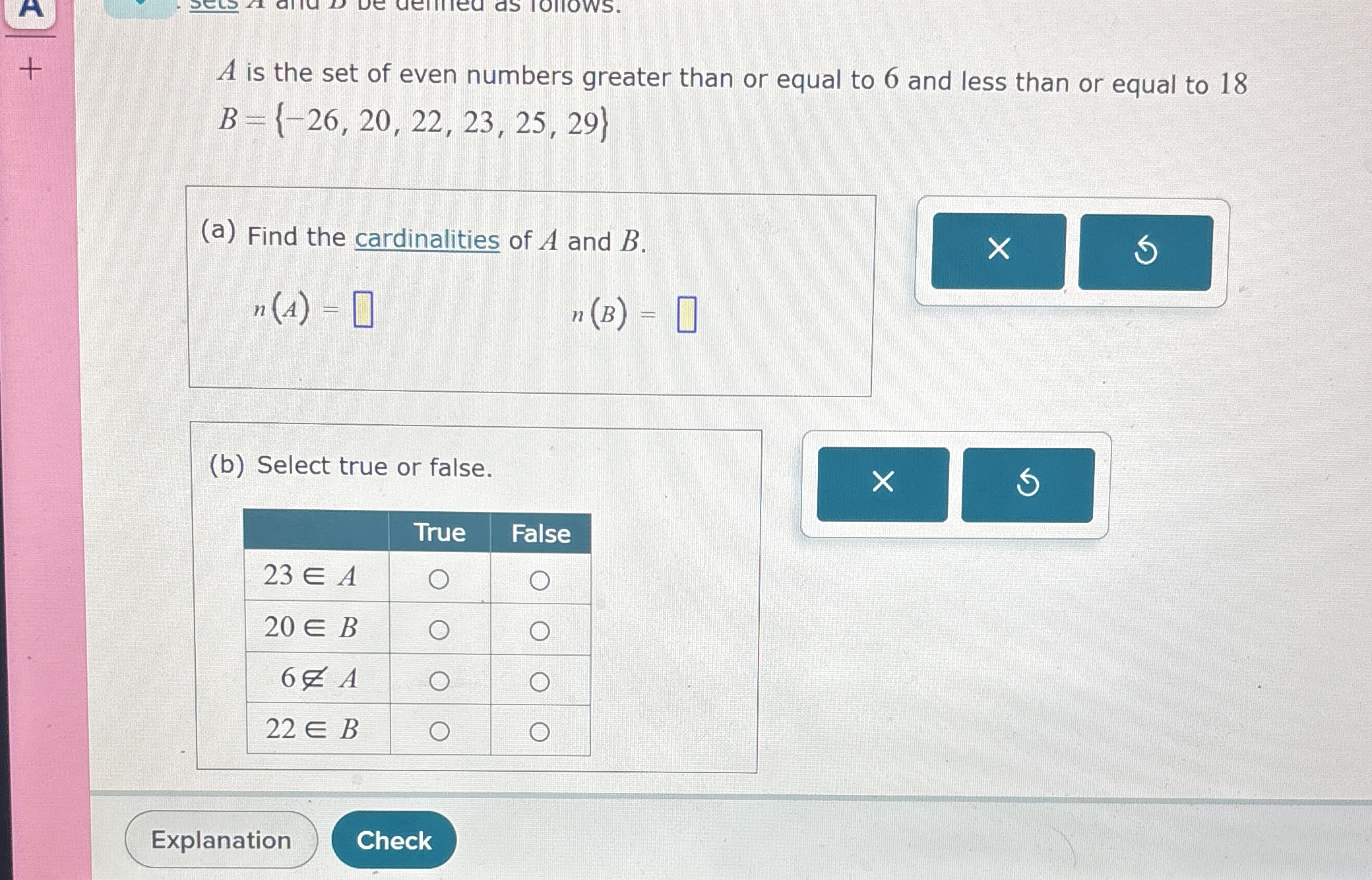
A is the set of even numbers greater than or equal to 6 and less than or equal to 18. B = {-26, 20, 22, 23, 25, 29}. (a) Find the cardinalities of A and B. n(A) = ? n(B) = ? (b)... A is the set of even numbers greater than or equal to 6 and less than or equal to 18. B = {-26, 20, 22, 23, 25, 29}. (a) Find the cardinalities of A and B. n(A) = ? n(B) = ? (b) Select true or false for the following statements: 23 ∈ A 20 ∈ B 6 ∉ A 22 ∈ B
Understand the Problem
The question defines two sets, A and B. It asks us to determmine the cardinalities of A and B, where A is the set of even numbers greater than or equal to 6 and less than or equal to 18, and B is a given set. We need to count the number of elements in each set. Then, we are asked to determine whether some elements are members of set A or set B.
Answer
n(A) = 7 n(B) = 6 $23 \in A$ is False $20 \in B$ is True $6 \notin A$ is False $22 \in B$ is True
Answer for screen readers
n(A) = 7 n(B) = 6 $23 \in A$ is False $20 \in B$ is True $6 \notin A$ is False $22 \in B$ is True
Steps to Solve
- Determine the elements of set A
Set A consists of even numbers greater than or equal to 6 and less than or equal to 18. Thus, $A = {6, 8, 10, 12, 14, 16, 18}$.
- Find the cardinality of set A
The cardinality of a set is the number of elements in the set. Since $A = {6, 8, 10, 12, 14, 16, 18}$, the number of elements in A is 7. Therefore, $n(A) = 7$.
- Find the cardinality of set B
The set B is given as $B = {-26, 20, 22, 23, 25, 29}$. The number of elements in B is 6. Therefore, $n(B) = 6$.
- Determine if 23 is an element of A
Since A only contains even numbers, and 23 is an odd number, $23 \notin A$. Therefore, the statement $23 \in A$ is false.
- Determine if 20 is an element of B
Looking at the set $B = {-26, 20, 22, 23, 25, 29}$, we can see that 20 is indeed an element of B. So, $20 \in B$ is true.
- Determine if 6 is not an element of A
We know that $A = {6, 8, 10, 12, 14, 16, 18}$. Since 6 is an element of A, the statement $6 \notin A$ is false.
- Determine if 22 is an element of B
Looking at the set $B = {-26, 20, 22, 23, 25, 29}$, we can see that 22 is an element of B. Therefore, $22 \in B$ is true.
n(A) = 7 n(B) = 6 $23 \in A$ is False $20 \in B$ is True $6 \notin A$ is False $22 \in B$ is True
More Information
The cardinality of a set represents the number of elements it contains. Element membership is determined by whether a particular element is found within the set's defined elements.
Tips
A common mistake could be miscounting the elements in set A or set B. Another mistake is confusing the $\in$ (is an element of) and $\notin$ (is not an element of) symbols.
AI-generated content may contain errors. Please verify critical information