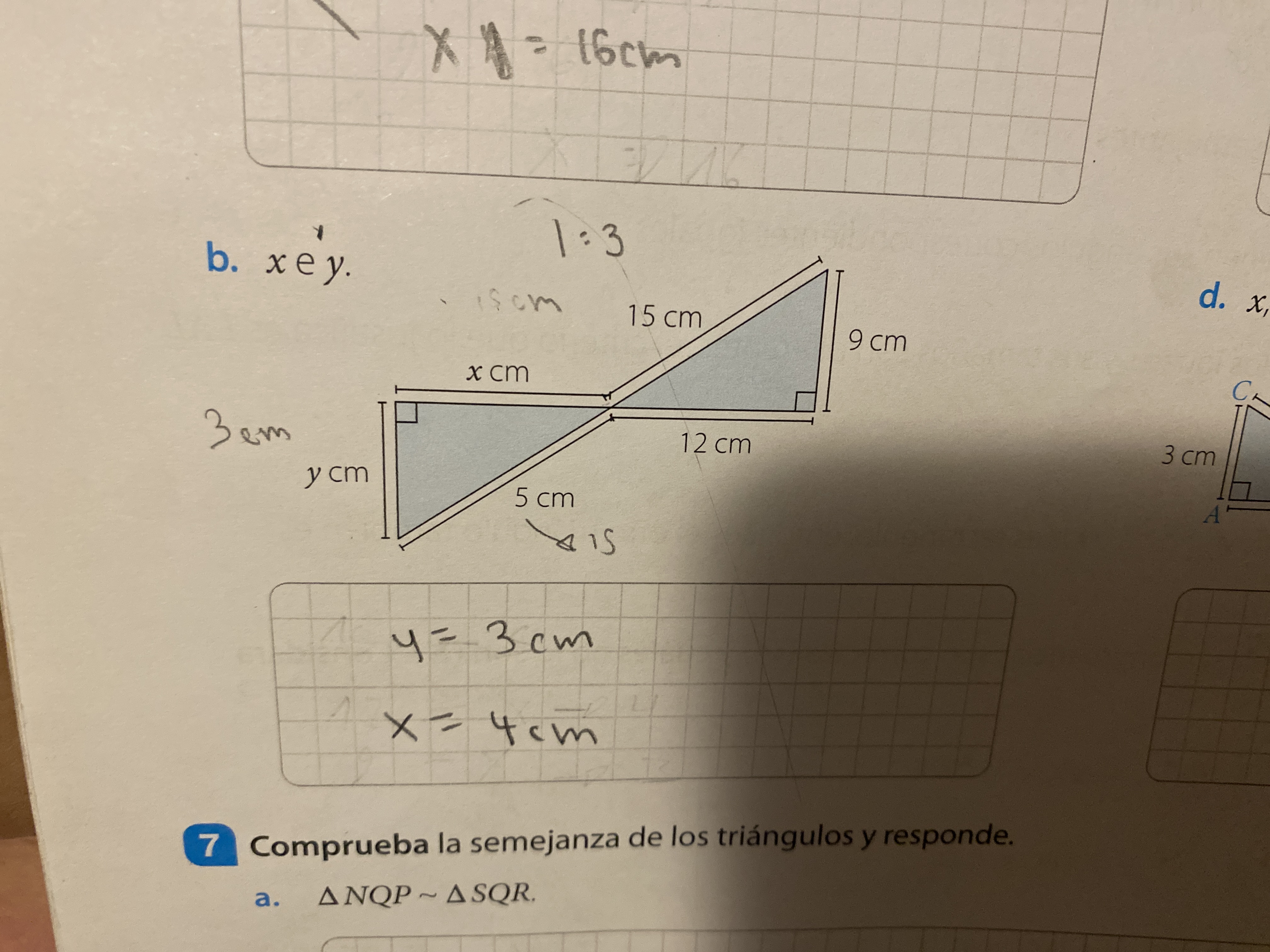
Encontrar los valores de x e y.
Understand the Problem
La pregunta pide determinar los valores de x y y en la figura dada, basándose en las relaciones geométricas entre los triángulos mostrados. Específicamente, se busca encontrar la longitud de los lados desconocidos de los triángulos.
Answer
$x = 4$ cm, $y = 3$ cm
Answer for screen readers
$x = 4$ cm, $y = 3$ cm
Steps to Solve
- Identify the similar triangles
The problem involves two right triangles that are similar because the angles at the intersection of their hypotenuses are vertical angles and therefore equal. Both triangles also have a right angle. By AA similarity, we know that the two triangles are similar.
- Set up the ratios for corresponding sides
Since the triangles are similar, the ratios of their corresponding sides are equal. We can set up the following proportions:
$$ \frac{y}{9} = \frac{5}{15} = \frac{x}{12} $$
- Solve for $y$
Using the proportion $\frac{y}{9} = \frac{5}{15}$, we solve for $y$:
$$ y = 9 \cdot \frac{5}{15} = 9 \cdot \frac{1}{3} = 3 $$
Therefore, $y = 3$ cm.
- Solve for $x$
Using the proportion $\frac{x}{12} = \frac{5}{15}$, we solve for $x$:
$$ x = 12 \cdot \frac{5}{15} = 12 \cdot \frac{1}{3} = 4 $$
Therefore, $x = 4$ cm.
$x = 4$ cm, $y = 3$ cm
More Information
The concept of similar triangles is widely used in geometry and trigonometry, especially in problems involving indirect measurements and scaling.
Tips
A common mistake is to mix up the corresponding sides when setting up the ratios. Ensure that the ratios are comparing sides in the correct order relative to the similar triangles.
AI-generated content may contain errors. Please verify critical information