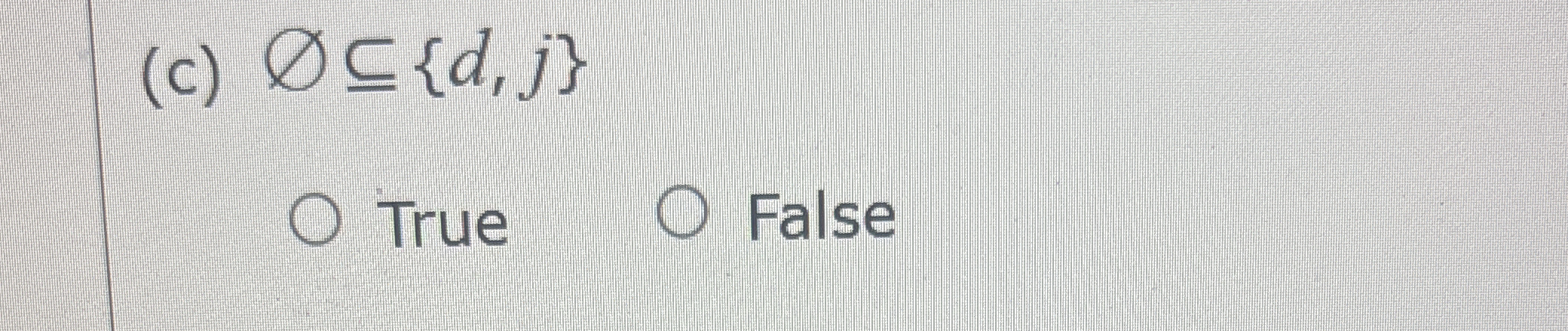
Is the empty set a subset of the set {d, j}?
Understand the Problem
The question is asking whether the empty set is a subset of the set containing 'd' and 'j'. In set theory, the empty set is a subset of every set.
Answer
True
Answer for screen readers
True
Steps to Solve
- Recall the definition of a subset
A set $A$ is a subset of a set $B$ if every element in $A$ is also in $B$.
- Understand the empty set
The empty set, denoted by $\emptyset$, is a set with no elements.
- Apply the subset definition to the empty set
Since the empty set has no elements, it vacuously satisfies the condition to be a subset of any set. There are no elements in the empty set that are not in ${d, j}$.
- Conclusion
Therefore, the empty set is a subset of ${d, j}$.
True
More Information
The empty set is a subset of every set, including itself.
Tips
A common mistake is thinking that because the empty set has no elements and ${d, j}$ has elements, the empty set cannot be a subset. However, the definition of a subset is satisfied because there isn't any element in the empty set that's not in ${d, j}$.
AI-generated content may contain errors. Please verify critical information