a) Use the sentence x^2 + 1/x^2 = 5 to evaluate the expression (x + 1/x)^2 b) Six people working 8 hours a day take ten days to finish a certain job. How long will it take for two... a) Use the sentence x^2 + 1/x^2 = 5 to evaluate the expression (x + 1/x)^2 b) Six people working 8 hours a day take ten days to finish a certain job. How long will it take for two people working 12 hours per day to finish the same job? c) The bank has a condition that on repaying back the borrowed loan the customer must be charged the interest rate of 8% per annum. John, the customer of the bank, borrowed shs. 28,000,000. How much did he own after two years and five months.
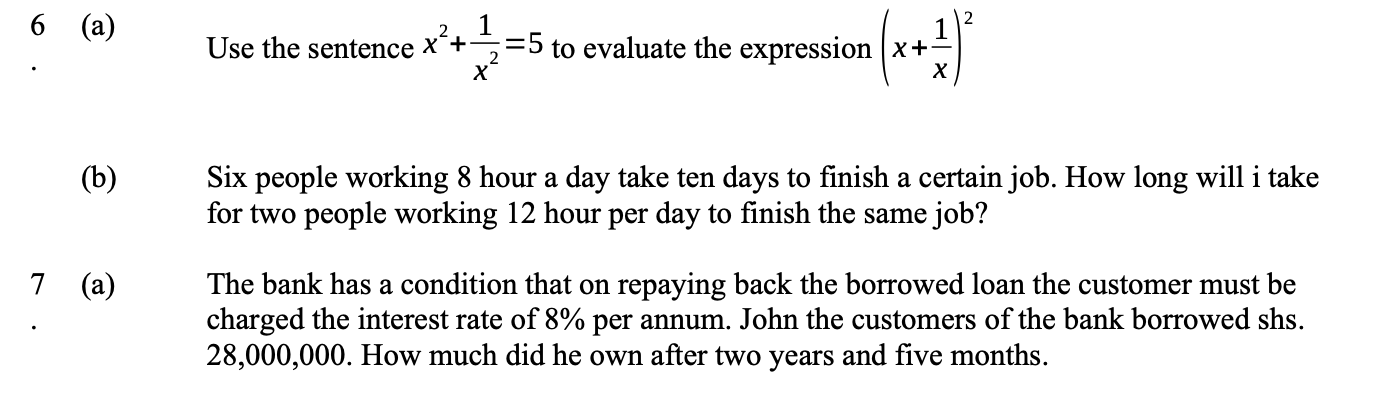
Understand the Problem
The image contains three math questions. Question 6(a) requires evaluating an expression given a condition. Question 6(b) is an inverse proportion problem related to work rate. Question 7(a) involves calculating the total amount owed after a certain period with compound interest.
Answer
6(a) 7 6(b) 20 days 7(a) shs. 33,712,000
Answer for screen readers
6(a) 7 6(b) 20 days 7(a) shs. 33,712,000
Steps to Solve
-
Expand the expression Expanding $(x + \frac{1}{x})^2$ we get: $(x + \frac{1}{x})^2 = x^2 + 2(x)(\frac{1}{x}) + \frac{1}{x^2} = x^2 + 2 + \frac{1}{x^2}$
-
Rearrange the equation Rearrange the terms to match the given equation $x^2 + \frac{1}{x^2} = 5$
$(x + \frac{1}{x})^2 = (x^2 + \frac{1}{x^2}) + 2$
- Substitute the given value Now substitute the value of $x^2 + \frac{1}{x^2}$ which is 5
$(x + \frac{1}{x})^2 = 5 + 2$
-
Simplify $(x + \frac{1}{x})^2 = 7$
-
Calculate total work done The total work done is given by the number of people multiplied by the number of hours they work per day, multiplied by the number of days. So, for the first scenario:
Total work = $6 \times 8 \times 10 = 480$ units
- Calculate the number of days for the second scenario Let the number of days be $d$. The total work done in the second scenario must equal the total work done in the first scenario:
$2 \times 12 \times d = 480$
-
Solve for d $24d = 480$ $d = \frac{480}{24}$ $d = 20$ days
-
Calculate the amount owed for compound interest
The formula for compound interest is: $A = P(1 + \frac{r}{n})^{nt}$ Where: $A =$ the future value of the investment/loan, including interest $P =$ the principal investment amount (the initial deposit or loan amount) $r =$ the annual interest rate (as a decimal) $n =$ the number of times that interest is compounded per year $t =$ the number of years the money is invested or borrowed for
In this case, $P = 28,000,000$, $r = 0.08$, and $n = 1$ (since it's compounded annually). The time period is 2 years and 5 months, which is $2 + \frac{5}{12} = 2.4167$ years (approximately). So $t \approx 2.4167$
Plugging in the values: $A = 28,000,000(1 + 0.08)^{(1 \times 2.4167)}$ $A = 28,000,000(1.08)^{2.4167}$ $A = 28,000,000 \times 1.204$ Approximately $A = 33,712,000$
6(a) 7 6(b) 20 days 7(a) shs. 33,712,000
More Information
The first question involves algebraic manipulation, the second deals with inverse proportionality. The third employs compound interest formula.
Tips
Null
AI-generated content may contain errors. Please verify critical information