In the last section, we defined the derivative of y = f(x) at the point x = x0 to be f'(x0) = lim(h->0) (f(x0 + h) - f(x0)) / h. We now investigate the derivative as a function der... In the last section, we defined the derivative of y = f(x) at the point x = x0 to be f'(x0) = lim(h->0) (f(x0 + h) - f(x0)) / h. We now investigate the derivative as a function derived from f by considering each point x in the domain of f.
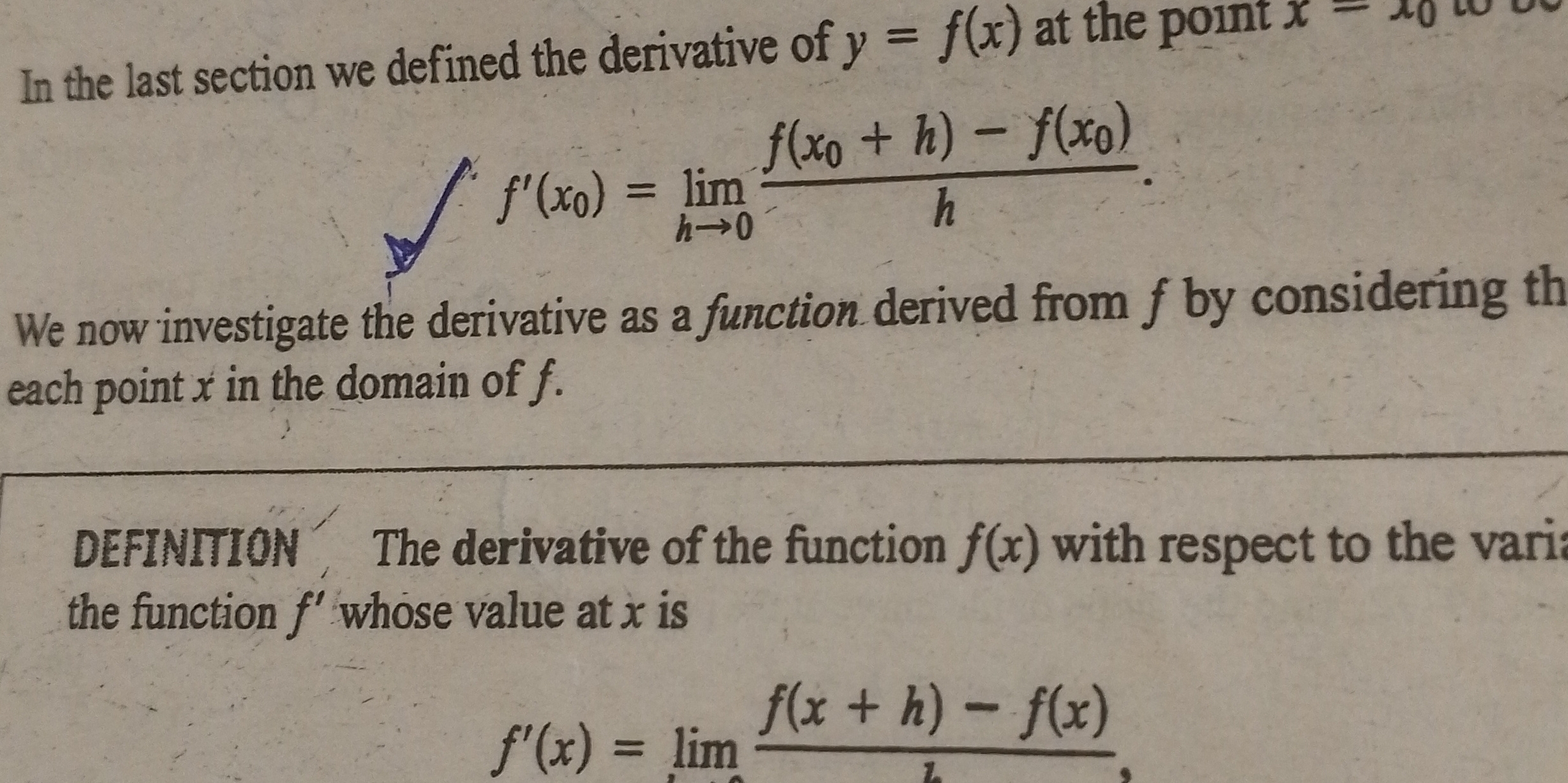
Understand the Problem
The question is discussing the definition of the derivative of a function in calculus, particularly focusing on its representation as a limit. It outlines how the derivative is expressed and introduces the concept of the derivative being a function derived from another function.
Answer
The derivative is given by $f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$.
Answer for screen readers
The derivative of the function $f(x)$ with respect to the variable $x$ is given by:
$$ f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} $$
Steps to Solve
- Understanding the Limit Definition of Derivative
The derivative of a function $f$ at a point $x_0$ can be expressed using the limit definition:
$$ f'(x_0) = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} $$
This formula measures the rate of change of the function at that specific point.
- Extending to the Derivative as a Function
To find the derivative as a function, we define $f'(x)$ as the derivative for any point $x$ in the domain of $f$:
$$ f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} $$
This means that for each point $x$ in the domain, we can evaluate the limit to get the derivative function.
- Wrap it up
By defining $f'(x)$ using the limit, we create a new function that tells us the slope of the original function $f(x)$ at any point $x$ in its domain.
The derivative of the function $f(x)$ with respect to the variable $x$ is given by:
$$ f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h} $$
More Information
The derivative describes how a function changes as its input changes. It's foundational in calculus, allowing the study of motion and rates of change, among other concepts.
Tips
- Mistaking the point of evaluation: Remember that $h$ approaches 0, so you're interested in the behavior at $x$, not just at $x_0$.
- Ignoring the limit: Always ensure to actually compute the limit when applying this definition.
AI-generated content may contain errors. Please verify critical information