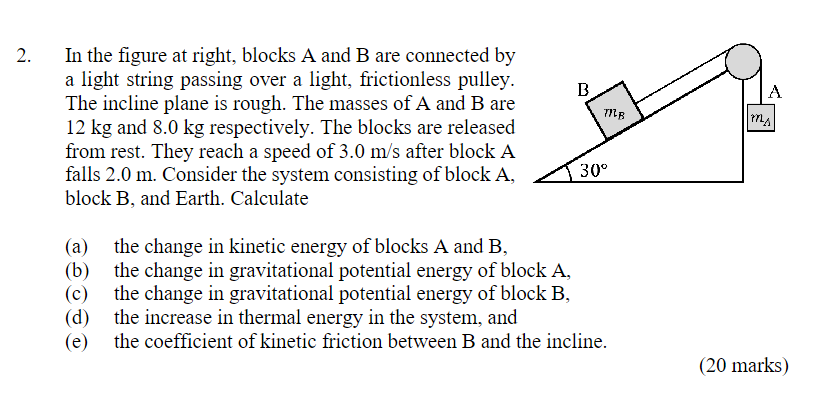
In the figure, blocks A and B are connected by a light string passing over a light, frictionless pulley. The incline plane is rough. The masses of A and B are 12 kg and 8.0 kg resp... In the figure, blocks A and B are connected by a light string passing over a light, frictionless pulley. The incline plane is rough. The masses of A and B are 12 kg and 8.0 kg respectively. The blocks are released from rest. They reach a speed of 3.0 m/s after block A falls 2.0 m. Consider the system consisting of block A, block B, and Earth. Calculate: (a) the change in kinetic energy of blocks A and B, (b) the change in gravitational potential energy of block A, (c) the change in gravitational potential energy of block B, (d) the increase in thermal energy in the system, and (e) the coefficient of kinetic friction between B and the incline.
Understand the Problem
The question describes a system involving two blocks (A and B) connected by a string over a pulley, with block B on an inclined plane. We are asked to calculate the change in kinetic energy of blocks A and B, the change in gravitational potential energy of block A, the change in gravitational potential energy of block B, the increase in thermal energy in the system, and the coefficient of kinetic friction between B and the incline.
Answer
(a) $ \Delta KE = 90 \text{ J} $ (b) $ \Delta PE_A = -235.2 \text{ J} $ (c) $ \Delta PE_B = 78.4 \text{ J} $ (d) $ \Delta E_{thermal} = 66.8 \text{ J} $ (e) $ \mu_k = 0.60 $
Answer for screen readers
(a) $ \Delta KE = 90 \text{ J} $ (b) $ \Delta PE_A = -235.2 \text{ J} $ (c) $ \Delta PE_B = 78.4 \text{ J} $ (d) $ \Delta E_{thermal} = 66.8 \text{ J} $ (e) $ \mu_k = 0.60 $
Steps to Solve
- Calculate the change in kinetic energy of blocks A and B
Since both blocks are connected by a string, they have the same speed. The total change in kinetic energy is the sum of the change in kinetic energy of each block: $ \Delta KE = \Delta KE_A + \Delta KE_B $ $ \Delta KE = \frac{1}{2} m_A v^2 + \frac{1}{2} m_B v^2 $ Where $m_A = 12 \text{ kg}$, $m_B = 8.0 \text{ kg}$, and $v = 3.0 \text{ m/s}$.
- Calculate the change in gravitational potential energy of block A
Block A falls a distance $h = 2.0 \text{ m}$. The change in gravitational potential energy is given by: $ \Delta PE_A = -m_A g h $ Where $g = 9.8 \text{ m/s}^2$. The negative sign indicates that the potential energy decreases as the block falls.
- Calculate the change in gravitational potential energy of block B
Block B moves up the incline. The vertical height increase is $ h = d \sin(\theta) $, where $ d = 2.0 \text{ m} $ is the distance block B travels along the incline, and $ \theta = 30^\circ $ is the angle of the incline. The change in gravitational potential energy of block B is: $ \Delta PE_B = m_B g h = m_B g d \sin(\theta) $
- Calculate the increase in thermal energy in the system
The increase in thermal energy is due to the work done by friction. According to the work-energy theorem, the change in mechanical energy is equal to the negative of the thermal energy generated due to friction. $ \Delta KE + \Delta PE_A + \Delta PE_B + \Delta E_{thermal} = 0 $ $ \Delta E_{thermal} = -(\Delta KE + \Delta PE_A + \Delta PE_B) $
- Calculate the coefficient of kinetic friction between B and the incline
The thermal energy generated is also equal to the work done by friction: $ \Delta E_{thermal} = f_k d $ Where $ f_k = \mu_k N $ is the kinetic friction force, $ \mu_k $ is coefficient of kinetic friction and $N $ is the normal force. The normal force is given by $N = m_B g \cos(\theta)$. Thus, $ \Delta E_{thermal} = \mu_k m_B g \cos(\theta) d $ Solving for $ \mu_k $: $ \mu_k = \frac{\Delta E_{thermal}}{m_B g \cos(\theta) d} $
(a) $ \Delta KE = 90 \text{ J} $ (b) $ \Delta PE_A = -235.2 \text{ J} $ (c) $ \Delta PE_B = 78.4 \text{ J} $ (d) $ \Delta E_{thermal} = 66.8 \text{ J} $ (e) $ \mu_k = 0.60 $
More Information
The problem combines concepts of kinetic energy, potential energy, and the work-energy theorem, along with frictional forces. Notice that the thermal energy generated is equal to the absolute value of the change in mechanical energy of the system.
Tips
- Incorrectly calculating the change in potential energy: Forgetting the negative sign for decreasing potential energy or not considering the angle of the incline when calculating the height change for block B.
- Incorrectly applying the work-energy theorem: Not including all energy changes in the system, especially the thermal energy due to friction.
- Incorrectly calculating the friction force: Not using the cosine of the angle to find the normal force.
- Units: Not using the correct units.
AI-generated content may contain errors. Please verify critical information