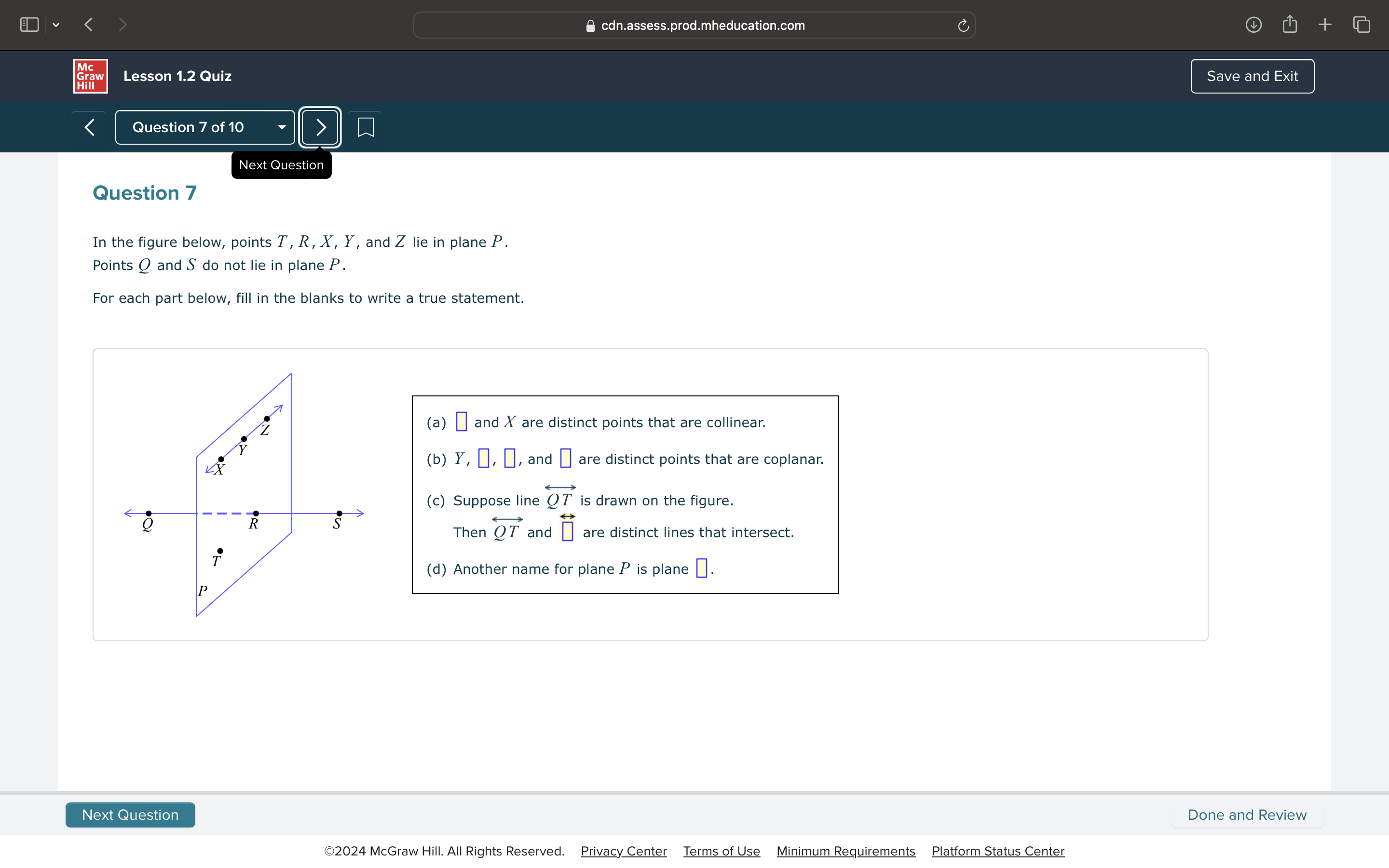
In the figure below, points T, R, X, Y, and Z lie in plane P. Points Q and S do not lie in plane P. For each part below, fill in the blanks to write a true statement. (a) and X are... In the figure below, points T, R, X, Y, and Z lie in plane P. Points Q and S do not lie in plane P. For each part below, fill in the blanks to write a true statement. (a) and X are distinct points that are collinear. (b) Y, , , and are distinct points that are coplanar. (c) Suppose line QT is drawn on the figure. Then QT and are distinct lines that intersect. (d) Another name for plane P is plane .
Understand the Problem
The question provides a geometric scenario involving points in a plane and asks to fill in the blanks to create true statements regarding collinearity, coplanarity, line intersections, and naming the plane. It requires interpreting the geometry provided in the figure.
Answer
(a) \( Y \) and \( X \) are distinct points that are collinear. (b) \( Y, R, T, \) and \( X \) are distinct points that are coplanar. (c) Suppose line \( \overline{QT} \) is drawn on the figure. Then \( \overline{QT} \) and \( \overline{RS} \) are distinct lines that intersect. (d) Another name for plane \( P \) is plane \( TR \).
Answer for screen readers
(a) ( Y ) and ( X ) are distinct points that are collinear.
(b) ( Y, R, T, ) and ( X ) are distinct points that are coplanar.
(c) Suppose line ( \overline{QT} ) is drawn on the figure. Then ( \overline{QT} ) and ( \overline{RS} ) are distinct lines that intersect.
(d) Another name for plane ( P ) is plane ( TR ).
Steps to Solve
-
Identify Collinearity for Part (a)
The points ( T ) and ( X ) lie in the plane ( P ). Generally, to say two points are collinear, you need to show they lie on the same line. In this case, since ( Y ) and ( X ) are both in ( P ) and are distinct points, they are collinear as part of a line in that plane. -
Determine Coplanarity for Part (b)
The points ( Y, R, T, ) and ( X ) are all in plane ( P ). Therefore, they are coplanar since they occupy the same plane. -
Analyze Line Intersections for Part (c)
Assuming line ( \overline{QT} ) is depicted, we need to determine if the lines intersect. The existence of point ( R ) in the line ( \overline{QT} ) suggests that the lines indeed intersect. -
Complete Plane Naming for Part (d)
Another name for plane ( P ) can be simply any two points that lie within it, such as ( T ) and ( R ). Thus, we can refer to plane ( P ) as plane ( TR ).
(a) ( Y ) and ( X ) are distinct points that are collinear.
(b) ( Y, R, T, ) and ( X ) are distinct points that are coplanar.
(c) Suppose line ( \overline{QT} ) is drawn on the figure. Then ( \overline{QT} ) and ( \overline{RS} ) are distinct lines that intersect.
(d) Another name for plane ( P ) is plane ( TR ).
More Information
This question revolves around fundamental concepts in geometry, particularly regarding points, lines, and planes. It assesses your understanding of collinearity (when points lie on the same line), coplanarity (when points lie within the same plane), and the relationships between lines and planes in a geometric context.
Tips
- Confusing collinearity with coplanarity: Ensure to differentiate between the two concepts.
- Assuming points or lines not clearly present in the diagram can be included without evidence: Always refer to what is specified in the figure.
- Misidentifying the plane's name using points not in the specified plane.
