Given W and Y are two events of an experiment with P(W) = 0.33, P(Y) = 0.42, and P(W∪Y) = 0.67, calculate the following probabilities: (a) P(Yᶜ) = ? (b) P(Wᶜ ∩ Yᶜ) = ? (c) P(Wᶜ ∪ Y... Given W and Y are two events of an experiment with P(W) = 0.33, P(Y) = 0.42, and P(W∪Y) = 0.67, calculate the following probabilities: (a) P(Yᶜ) = ? (b) P(Wᶜ ∩ Yᶜ) = ? (c) P(Wᶜ ∪ Yᶜ) = ?
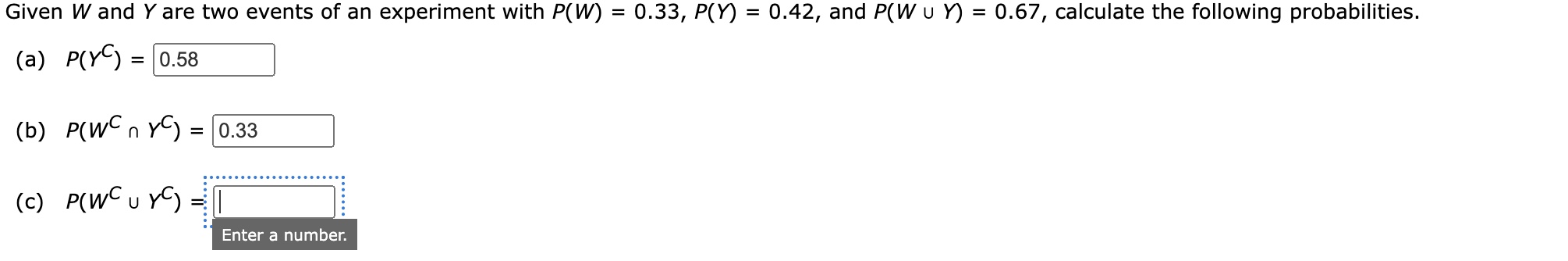
Understand the Problem
The question is asking to calculate probabilities related to events W and Y, given P(W), P(Y), and P(W union Y). Specifically, it asks to calculate P(Y complement), P(W complement intersect Y complement), and P(W complement union Y complement).
Answer
$P(W^C \cup Y^C) = 0.92$
Answer for screen readers
$P(W^C \cup Y^C) = 0.92$
Steps to Solve
-
Find $P(W^C \cup Y^C)$ using De Morgan's Law
De Morgan's Law states that $(W \cap Y)^C = W^C \cup Y^C$. Thus, $P(W^C \cup Y^C) = P((W \cap Y)^C)$. We can find $P((W \cap Y)^C)$ by using the formula $P(A^C) = 1 - P(A)$. Therefore, $P((W \cap Y)^C) = 1 - P(W \cap Y)$.
-
Find $P(W \cap Y)$ using the formula for $P(W \cup Y)$
The formula $P(W \cup Y) = P(W) + P(Y) - P(W \cap Y)$ can be rearranged to find $P(W \cap Y)$:
$P(W \cap Y) = P(W) + P(Y) - P(W \cup Y)$.
Plug in the given values:
$P(W \cap Y) = 0.33 + 0.42 - 0.67 = 0.08$.
-
Calculate $P(W^C \cup Y^C)$
Now that we have $P(W \cap Y) = 0.08$, we can find $P(W^C \cup Y^C) = 1 - P(W \cap Y)$:
$P(W^C \cup Y^C) = 1 - 0.08 = 0.92$.
$P(W^C \cup Y^C) = 0.92$
More Information
De Morgan's Laws are a pair of rules in probability and set theory that relate the complements of unions and intersections. They are very useful in simplifying complex probability calculations.
Tips
A common mistake is to confuse the union and intersection symbols and their properties or to incorrectly apply De Morgan's Laws. Another mistake is to forget to use the complement rule correctly when calculating probabilities of complementary events.
AI-generated content may contain errors. Please verify critical information