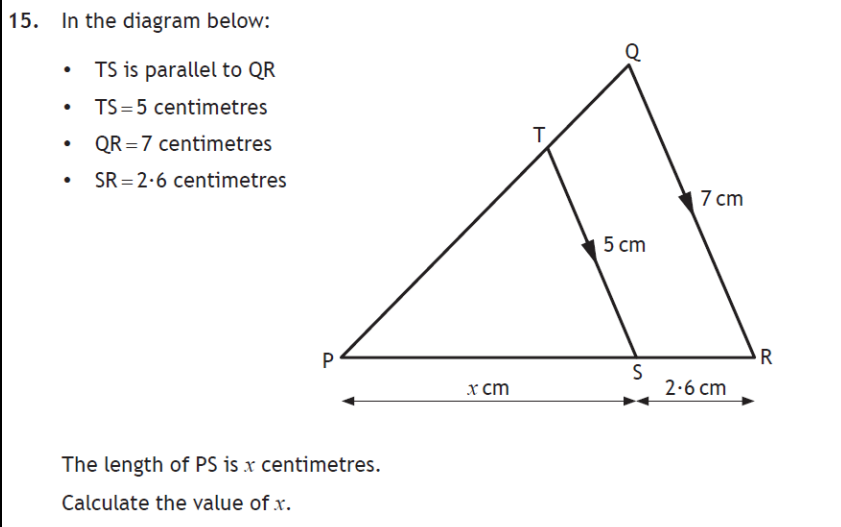
In the diagram below, TS is parallel to QR, TS = 5 cm, QR = 7 cm, and SR = 2.6 cm. The length of PS is x cm. Calculate the value of x.

Steps to Solve

1. Recognize similar triangles

Since $TS$ is parallel to $QR$, triangle $PTS$ is similar to triangle $PQR$. This is due to the AA (Angle-Angle) similarity postulate: $\angle PTS = \angle PQR$ and $\angle PST = \angle PRQ$ because they are corresponding angles formed by parallel lines $TS$ and $QR$ cut by transversals $PT$ and $PR$ respectively. Also, $\angle P$ is common to both triangles.

2. Set up a proportion using corresponding sides

We can set up a proportion relating the corresponding sides of the similar triangles $PTS$ and $PQR$. Specifically, we can relate the lengths $TS$ and $QR$ to the lengths $PS$ and $PR$. We know $TS = 5$, $QR = 7$, $PS = x$, and $SR = 2.6$. Also, $PR = PS + SR = x + 2.6$. Therefore the proportion is: $$ \frac{TS}{QR} = \frac{PS}{PR} $$ $$ \frac{5}{7} = \frac{x}{x + 2.6} $$

3. Solve for x

Cross-multiply to solve for x: $$ 5(x + 2.6) = 7x $$ $$ 5x + 13 = 7x $$ $$ 13 = 2x $$ $$ x = \frac{13}{2} $$ $$ x = 6.5 $$