If f(x, y) = (1/√y) e^(-(x-a)²/4t), find f(x, y) = f(c, y_n).
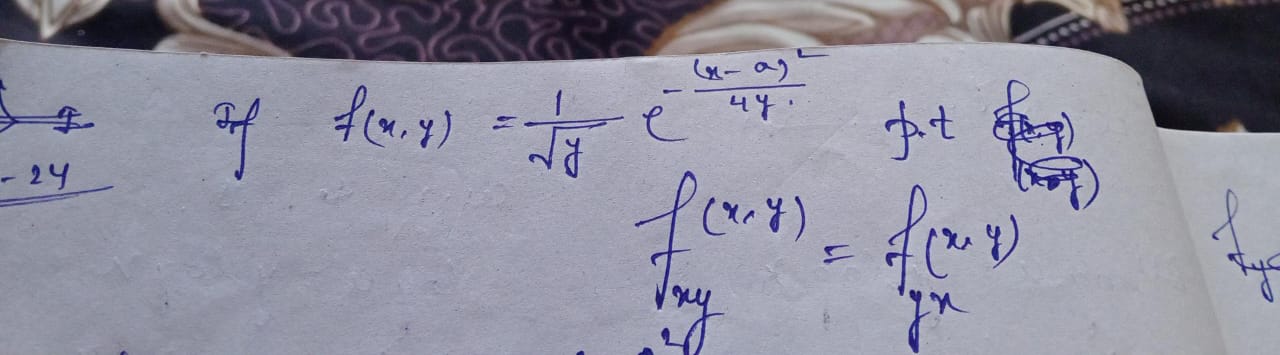
Understand the Problem
The question involves a mathematical function in two variables, specifically a function denoted by f(x, y) and its relation to some exponential function involving variables x, a, and y. The expression indicates a potentially complex calculus or differential equations problem, likely requiring steps to analyze or solve for certain conditions or transformations.
Answer
$$ y = y_n e^{-\frac{(c-a)^2 - (x-a)^2}{4t}} $$
Answer for screen readers
The expression for $y$ is: $$ y = y_n e^{-\frac{(c-a)^2 - (x-a)^2}{4t}} $$
Steps to Solve
-
Set the equation for f(x, y) We start with the given function: $$ f(x, y) = \frac{1}{\sqrt{y}} e^{-\frac{(x-a)^2}{4t}} $$
-
Substitute f(c, y_n) We want to equate the function at a specific point: $$ f(c, y_n) = \frac{1}{\sqrt{y_n}} e^{-\frac{(c-a)^2}{4t}} $$
-
Equate both expressions Set the two expressions equal to each other: $$ \frac{1}{\sqrt{y}} e^{-\frac{(x-a)^2}{4t}} = \frac{1}{\sqrt{y_n}} e^{-\frac{(c-a)^2}{4t}} $$
-
Cross-multiply to simplify To get rid of the fractions, cross-multiply: $$ \sqrt{y_n} e^{-\frac{(x-a)^2}{4t}} = \sqrt{y} e^{-\frac{(c-a)^2}{4t}} $$
-
Isolate y on one side Rearranging gives: $$ \frac{y_n}{y} = e^{\frac{(c-a)^2 - (x-a)^2}{4t}} $$
-
Express y in terms of other variables This leads us to express $y$ in terms of $y_n$, $x$, $c$, $a$, and $t$: $$ y = y_n e^{-\frac{(c-a)^2 - (x-a)^2}{4t}} $$
The expression for $y$ is: $$ y = y_n e^{-\frac{(c-a)^2 - (x-a)^2}{4t}} $$
More Information
This result shows how the variable $y$ is influenced by the input parameters $y_n$, the spatial parameters $c$ and $x$, the constant $a$, and the time variable $t$. The exponential term indicates a decay or growth factor depending on the relation of $(c-a)^2$ and $(x-a)^2$.
Tips
- Forgetting to appropriately substitute values: It's crucial to substitute correctly to maintain equality throughout the manipulation of equations.
- Misapplying logarithms: When dealing with exponential functions, careful handling of logarithmic properties is necessary.
AI-generated content may contain errors. Please verify critical information