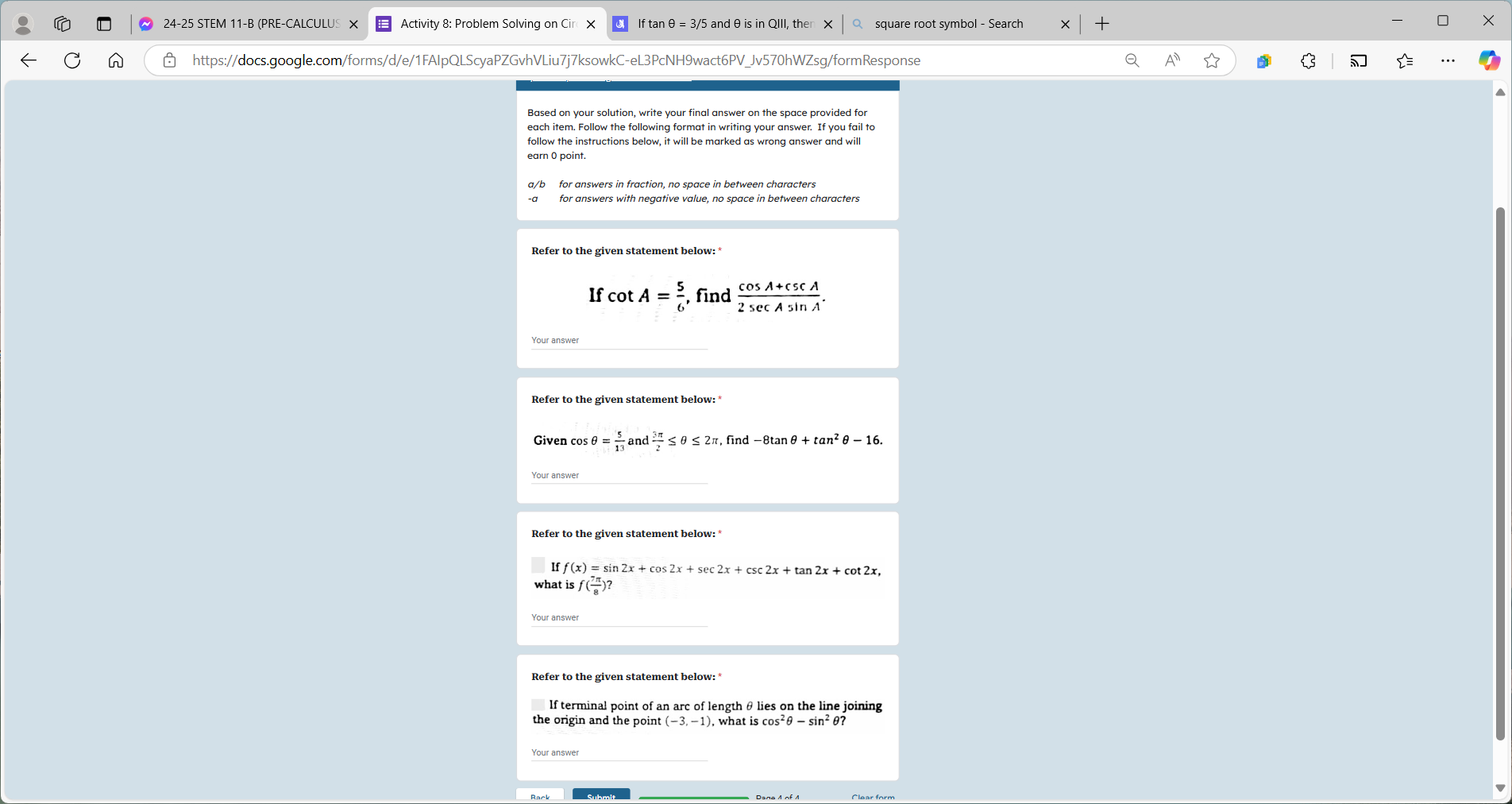
If cot A = 5/6, find cos A + csc A. Given cos θ = 1/3 and -π/2 ≤ θ ≤ 2π, find -8tan²θ - 16. If f(x) = sin 2x + cos 2x + sec 2x + csc 2x + tan 2x, what is f(π/3)? If terminal point... If cot A = 5/6, find cos A + csc A. Given cos θ = 1/3 and -π/2 ≤ θ ≤ 2π, find -8tan²θ - 16. If f(x) = sin 2x + cos 2x + sec 2x + csc 2x + tan 2x, what is f(π/3)? If terminal point of an arc of length θ lies on the line joining the origin and the point (-3,-1), what is cos²θ - sin²θ? Read more

Steps to Solve

1. Calculate Values from Given Information

   For ( \cot A = \frac{5}{6} ), we can find ( \sin A ) and ( \cos A ).

   Using the identity ( \cot A = \frac{\cos A}{\sin A} ), we write $$ \cos A = 5k \quad \text{and} \quad \sin A = 6k $$ where ( k ) is a common factor. By the Pythagorean theorem, $$ \cos^2 A + \sin^2 A = 1 $$

   Substituting gives: $$ (5k)^2 + (6k)^2 = 1 \implies 25k^2 + 36k^2 = 1 \implies 61k^2 = 1 \implies k^2 = \frac{1}{61} \implies k = \frac{1}{\sqrt{61}} $$

   Hence, $$ \cos A = \frac{5}{\sqrt{61}}, \quad \sin A = \frac{6}{\sqrt{61}} $$

2. Use the Formulas for ( \cos(A+C) ) and ( \sin(A) )

   We need ( \cos A + \csc A ) and ( 2 \sec A \sin A ). First, $$ \csc A = \frac{1}{\sin A} = \frac{\sqrt{61}}{6} $$ Therefore, $$ \cos A + \csc A = \frac{5}{\sqrt{61}} + \frac{\sqrt{61}}{6} $$

   To combine, find a common denominator (use ( 6\sqrt{61} )): $$ = \frac{30 + 61}{6\sqrt{61}} = \frac{91}{6\sqrt{61}} $$

3. Calculate ( 2 \sec A \sin A )

   First, find ( \sec A ): $$ \sec A = \frac{1}{\cos A} = \frac{\sqrt{61}}{5} $$ Thus, $$ 2 \sec A \sin A = 2 \cdot \frac{\sqrt{61}}{5} \cdot \frac{6}{\sqrt{61}} = \frac{12}{5} $$

4. Final Calculation of the Required Expression

   Now substitute these into the required result: $$ \cos A + \csc A - 2 \sec A \sin A = \frac{91}{6\sqrt{61}} - \frac{12}{5} $$

   To combine, use the least common multiple for denominators: $$ = \frac{91 \cdot 5 - 12 \cdot 6\sqrt{61}}{30\sqrt{61}} $$ Calculating this gives: $$ \frac{455 - 72\sqrt{61}}{30\sqrt{61}} $$

5. Conclusion

   The final result is: $$ \frac{455 - 72\sqrt{61}}{30\sqrt{61}} $$