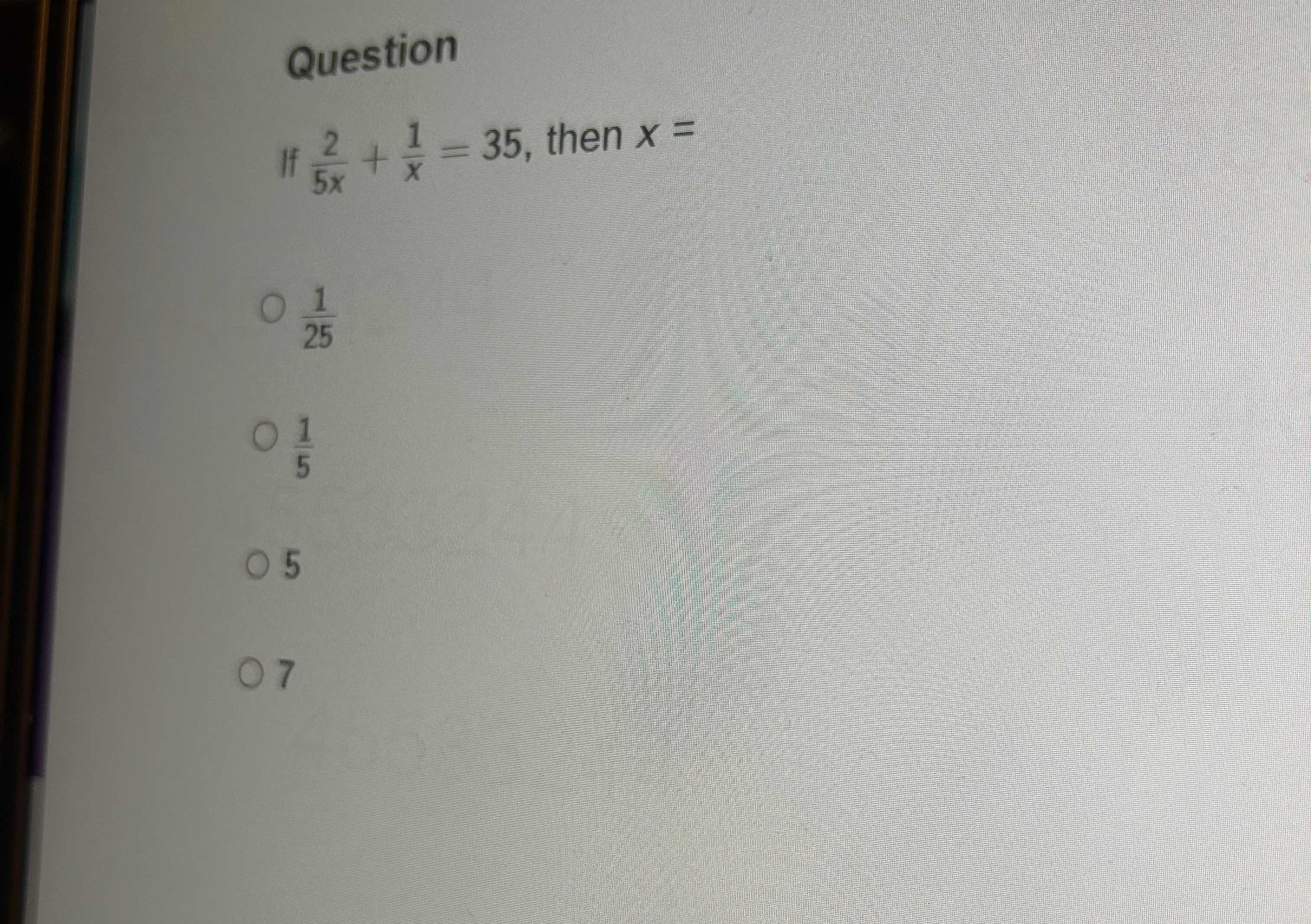
If 2/(5x) + 1/x = 35, then x =
Understand the Problem
The question is asking for the value of x in the equation 2/(5x) + 1/x = 35. We will need to solve this equation step by step to find the value of x.
Answer
The solution is \( x = \frac{1}{25} \).
Answer for screen readers
The value of ( x ) is ( \frac{1}{25} ).
Steps to Solve
- Combine the fractions on the left side
To solve the equation
$$ \frac{2}{5x} + \frac{1}{x} = 35, $$
we first need a common denominator for the fractions on the left. The common denominator is ( 5x ). We rewrite the second fraction:
$$ \frac{1}{x} = \frac{5}{5x}. $$
Now the equation becomes:
$$ \frac{2}{5x} + \frac{5}{5x} = 35. $$
- Add the fractions
Now that we have a common denominator, we can combine the fractions:
$$ \frac{2 + 5}{5x} = 35. $$
This simplifies to:
$$ \frac{7}{5x} = 35. $$
- Clear the fraction
Next, we can eliminate the fraction by multiplying both sides by ( 5x ):
$$ 7 = 35(5x). $$
- Solve for ( x )
Now, simplify the right side:
$$ 7 = 175x. $$
To isolate ( x ), divide both sides by 175:
$$ x = \frac{7}{175}. $$
- Simplify the fraction
Now we can simplify ( \frac{7}{175} ):
$$ x = \frac{1}{25}. $$
The value of ( x ) is ( \frac{1}{25} ).
More Information
The answer ( \frac{1}{25} ) shows how to handle equations with fractions and emphasizes the importance of finding a common denominator. Reducing the fraction is also a key step in arriving at the simplest form.
Tips
- Forgetting to find a common denominator when adding fractions.
- Not clearing fractions properly by multiplying both sides by the denominator.
AI-generated content may contain errors. Please verify critical information