If $(2^{3x-1} + 10) / 7 = 6$, then what is the value of x?
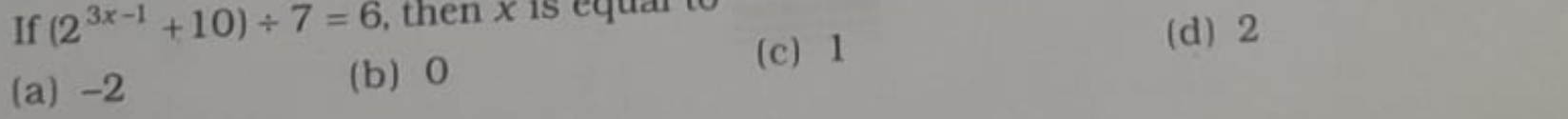
Understand the Problem
The question asks us to solve the exponential equation (2^(3x-1) + 10) / 7 = 6 for the variable x. We'll need to isolate the exponential term and then use logarithms to solve for x.
Answer
(d) $2$
Answer for screen readers
(d) $2$
Steps to Solve
- Isolate the term with the exponent
First, we need to isolate the exponential term. The equation is:
$$(2^{3x-1} + 10) / 7 = 6$$
Multiply both sides by 7:
$$2^{3x-1} + 10 = 6 \cdot 7$$
$$2^{3x-1} + 10 = 42$$
- Continue isolating the exponential
Subtract 10 from both sides:
$$2^{3x-1} = 42 - 10$$
$$2^{3x-1} = 32$$
- Express 32 as a power of 2
We can express 32 as $2^5$:
$$2^{3x-1} = 2^5$$
- Equate the exponents
Since the bases are equal, we can equate the exponents:
$$3x - 1 = 5$$
- Solve for x
Add 1 to both sides:
$$3x = 5 + 1$$
$$3x = 6$$
Divide both sides by 3:
$$x = \frac{6}{3}$$
$$x = 2$$
(d) $2$
More Information
The value of $x$ that satisfies the equation $(2^{3x-1} + 10) / 7 = 6$ is $x = 2$. We found this by isolating the exponential term and using the property that if $a^m = a^n$, then $m = n$.
Tips
A common mistake is to incorrectly apply the order of operations when isolating the exponential term. For example, some might subtract 10 before multiplying by 7. Another error could be made while solving for $x$ in the linear equation $3x - 1 = 5$.
AI-generated content may contain errors. Please verify critical information