Solve the following quadratic equation for x: (a+b)x² + (a+2b+c)x + (b+c) = 0
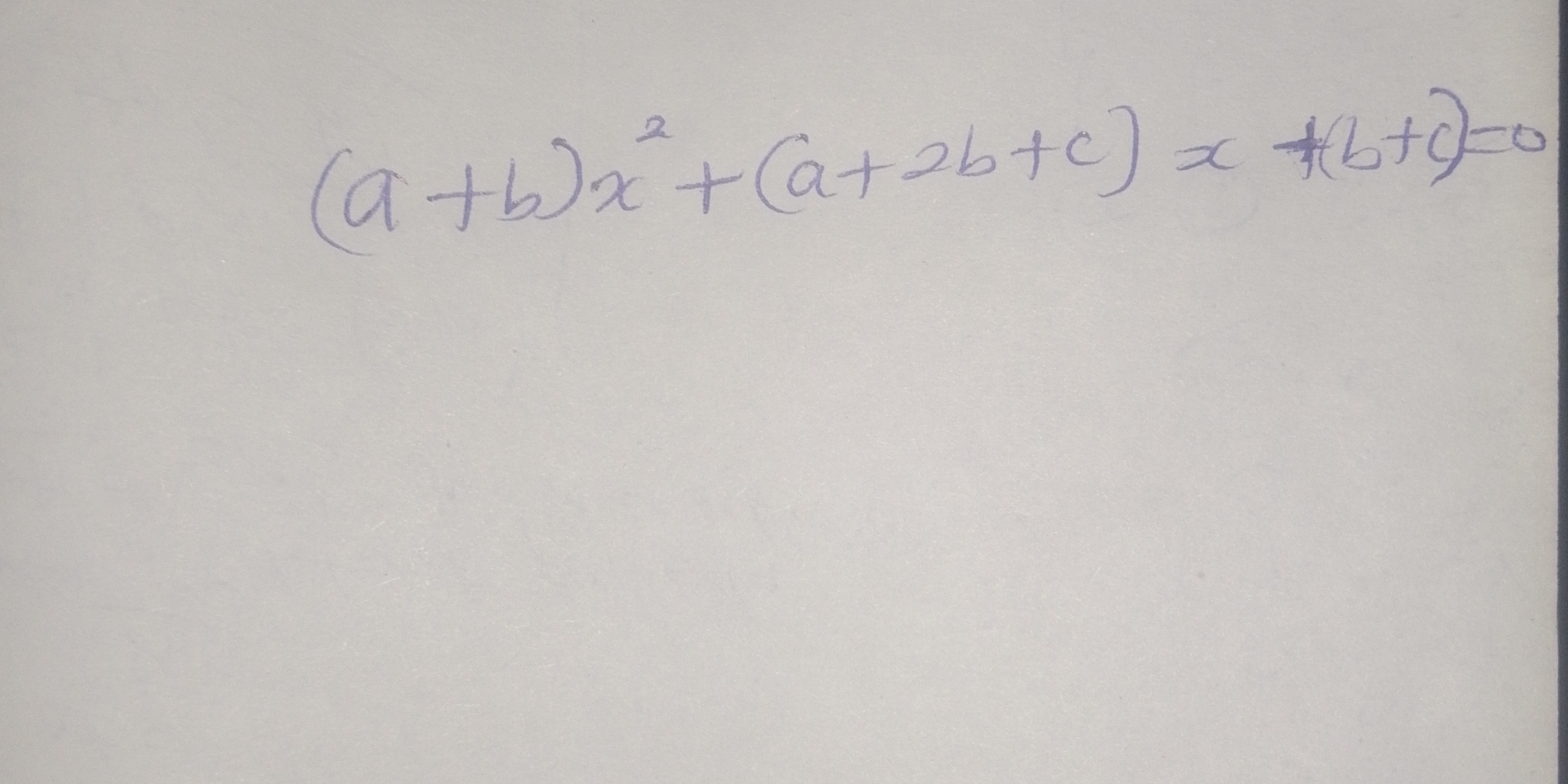
Understand the Problem
The question appears to present a quadratic equation in terms of variables a, b, and c, and asks us to solve for x. You need to provide the full question so I can completely address it.
Answer
$x = -1, -\frac{b+c}{a+b}$
Answer for screen readers
$x = -1, -\frac{b+c}{a+b}$
Steps to Solve
- Rewrite the equation
The equation is $(a+b)x^2 + (a+2b+c)x + (b+c) = 0$.
- Factor by grouping
We attempt to factor the quadratic expression by grouping. We are looking for two numbers that multiply to $(a+b)(b+c)$ and add up to $a+2b+c$. Notice that $(a+b)+(b+c) = a+2b+c$. This suggests that we can split the middle term as follows: $(a+b)x^2 + (a+b)x + (b+c)x + (b+c) = 0$
- Factor out common terms
Factor $(a+b)x$ from the first two terms and $(b+c)$ from the last two terms: $(a+b)x(x+1) + (b+c)(x+1) = 0$
- Factor out $(x+1)$
Now we can factor out the common term $(x+1)$: $((a+b)x + (b+c))(x+1) = 0$
- Solve for $x$
To find the solutions for $x$, we set each factor equal to zero: $(a+b)x + (b+c) = 0$ or $(x+1) = 0$
From the second equation, we have $x = -1$.
From the first equation, we have $(a+b)x = -(b+c)$, so $x = -\frac{b+c}{a+b}$.
$x = -1, -\frac{b+c}{a+b}$
More Information
These are the two solutions to the quadratic equation. Note that if $a = -b$, the second solution is undefined, and the original equation reduces to $(b+c) = 0$, which is not a quadratic equation anymore.
Tips
A common mistake would be to try to directly apply the quadratic formula, which would lead to a very complicated expression that is difficult to simplify. Factoring by grouping is a more efficient method in this case. Another common mistake is to not consider both possible solutions arising from the factored equation.
AI-generated content may contain errors. Please verify critical information