HW U(x) = sin^{-1}(x) + (π/2 - 1)x - ∫ t u(t) dt
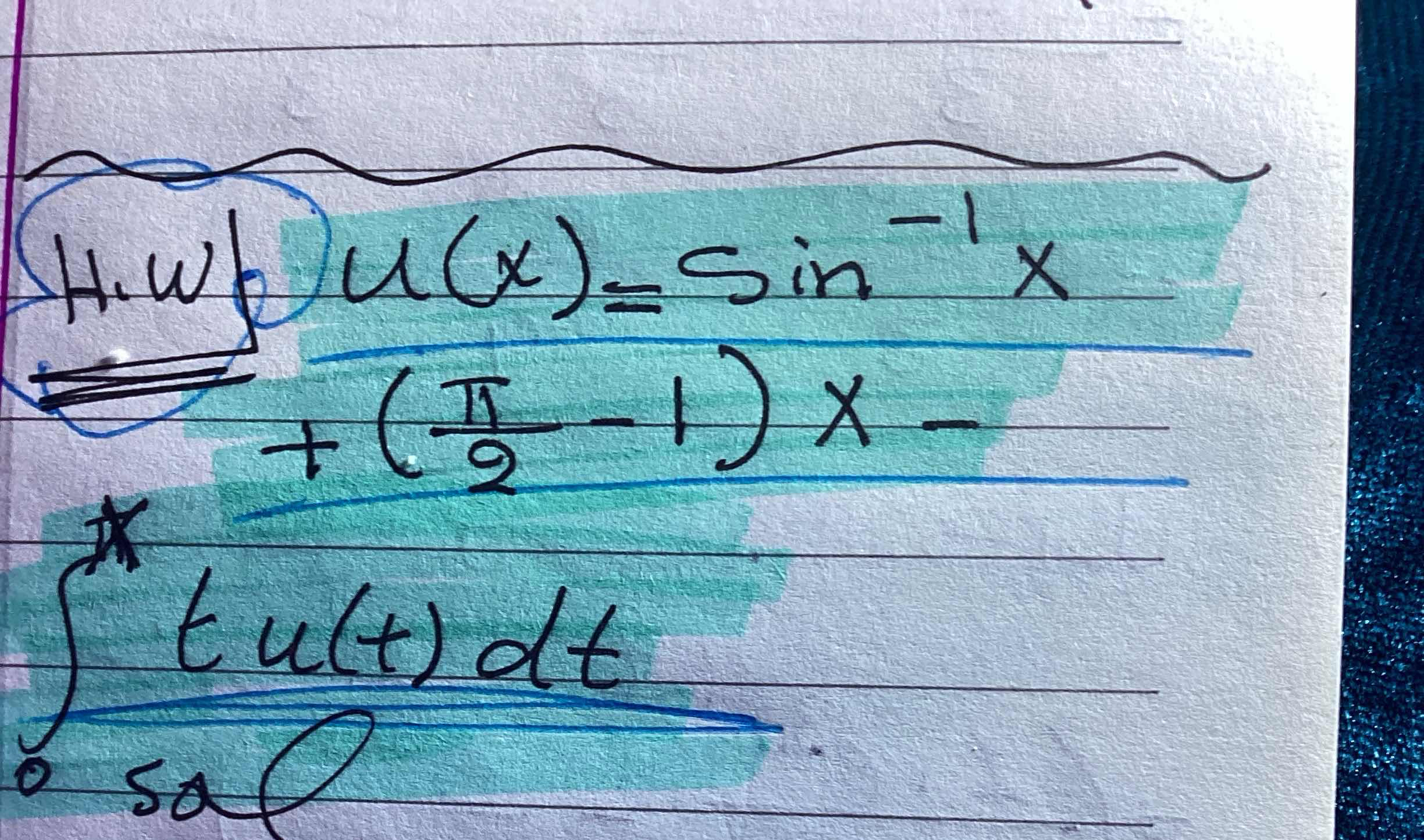
Understand the Problem
The question presents an expression involving the function u(x) defined as sin^{-1}(x) along with an integral involving t u(t) dt. It appears to be related to integration or manipulation of functions in calculus.
Answer
The function is given as: $$ U(x) = \sin^{-1}(x) + \left(\frac{\pi}{2} - 1\right)x - \int_{0}^{x} t u(t) \, dt $$
Answer for screen readers
The function ( U(x) ) is: $$ U(x) = \sin^{-1}(x) + \left(\frac{\pi}{2} - 1\right)x - \left( \frac{x^2}{2} \sin^{-1}(x) - \text{[evaluated integral]} + \left(\frac{\pi}{2} - 1\right) \cdot \frac{x^3}{3} \right) $$
Steps to Solve
- Identify the given function and integral
The function given is: $$ U(x) = \sin^{-1}(x) + \left(\frac{\pi}{2} - 1\right)x - \int_{0}^{x} t u(t) , dt $$
Where ( u(t) = \sin^{-1}(t) + \left(\frac{\pi}{2} - 1\right)t ).
- Substitute ( u(t) ) into the integral
Replace ( u(t) ) with ( \sin^{-1}(t) + \left(\frac{\pi}{2} - 1\right)t ): $$ U(x) = \sin^{-1}(x) + \left(\frac{\pi}{2} - 1\right)x - \int_{0}^{x} t \left(\sin^{-1}(t) + \left(\frac{\pi}{2} - 1\right)t \right) dt $$
- Distribute ( t ) in the integral
Now split the integral into two parts: $$ \int_{0}^{x} t \sin^{-1}(t) , dt + \int_{0}^{x} \left(\frac{\pi}{2} - 1\right) t^2 , dt $$
- Solve the first integral ( \int_{0}^{x} t \sin^{-1}(t) , dt )
This might require integration by parts. Let ( u = \sin^{-1}(t) ), so ( du = \frac{1}{\sqrt{1 - t^2}} dt ) and ( dv = t dt ), giving ( v = \frac{t^2}{2} ).
Using integration by parts: $$ \int t \sin^{-1}(t) , dt = \frac{t^2}{2} \sin^{-1}(t) - \int \frac{t^2}{2\sqrt{1-t^2}} , dt $$
- Evaluate the second integral ( \int_{0}^{x} \left(\frac{\pi}{2} - 1\right) t^2 , dt )
This evaluates to: $$ \left(\frac{\pi}{2} - 1\right) \cdot \frac{x^3}{3} $$
- Combine results and simplify
Substituting the result of the integrals back into ( U(x) ) and simplifying gives you the final form of ( U(x) ).
The function ( U(x) ) is: $$ U(x) = \sin^{-1}(x) + \left(\frac{\pi}{2} - 1\right)x - \left( \frac{x^2}{2} \sin^{-1}(x) - \text{[evaluated integral]} + \left(\frac{\pi}{2} - 1\right) \cdot \frac{x^3}{3} \right) $$
More Information
This expression involves integrating a composite function and utilizing integration by parts. The result shows the relationship between the function (U(x)) and its components, linking it back to (u(t)).
Tips
- Forgetting to properly apply integration by parts or misidentifying ( u ) and ( dv ).
- Neglecting the limits of integration when switching from indefinite to definite integrals.
- Incorrectly evaluating the integral of ( t^2 ).
AI-generated content may contain errors. Please verify critical information