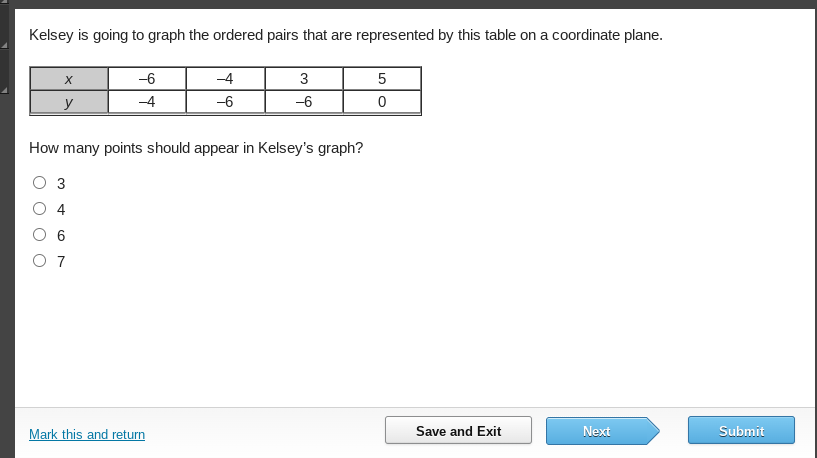
How many points should appear in Kelsey's graph?
Understand the Problem
The question is asking how many unique ordered pairs (x, y) can be derived from the given table to graph them on a coordinate plane. The focus is on counting distinct pairs without repetition.
Answer
4
Answer for screen readers
There are 4 unique ordered pairs in Kelsey's graph.
Steps to Solve
- Identify Ordered Pairs
We are given a table with $x$ and $y$ values:
[ \begin{array}{c|cccc} x & -6 & -4 & 3 & 5 \ \hline y & -4 & -6 & -6 & 0 \ \end{array} ]
From this table, we can create the following ordered pairs (x, y):
- From $x = -6$, $y = -4$: Pair is $(-6, -4)$
- From $x = -4$, $y = -6$: Pair is $(-4, -6)$
- From $x = 3$, $y = -6$: Pair is $(3, -6)$
- From $x = 5$, $y = 0$: Pair is $(5, 0)$
- List All Ordered Pairs
Now we list each ordered pair:
- $(-6, -4)$
- $(-4, -6)$
- $(3, -6)$
- $(5, 0)$
- Check for Uniqueness
Now we need to check for unique ordered pairs.
Comparing the pairs, we find that:
- $(-6, -4) \neq (-4, -6)$
- $(-6, -4) \neq (3, -6)$
- $(-6, -4) \neq (5, 0)$
- $(-4, -6) \neq (3, -6)$
- $(-4, -6) \neq (5, 0)$
- $(3, -6) \neq (5, 0)$
All pairs are unique.
- Count Unique Ordered Pairs
Since all pairs are unique, we count the total:
Total unique ordered pairs = 4.
There are 4 unique ordered pairs in Kelsey's graph.
More Information
The four unique ordered pairs were created from distinct $x$ and $y$ values. Each ordered pair represents a unique point on the Cartesian coordinate plane.
Tips
- Forgetting to check if pairs are unique, leading to over-counting. Always compare each pair to ensure they are distinct.
- Misreading the table and misinterpreting the pairs. Double-check the values in the table.
