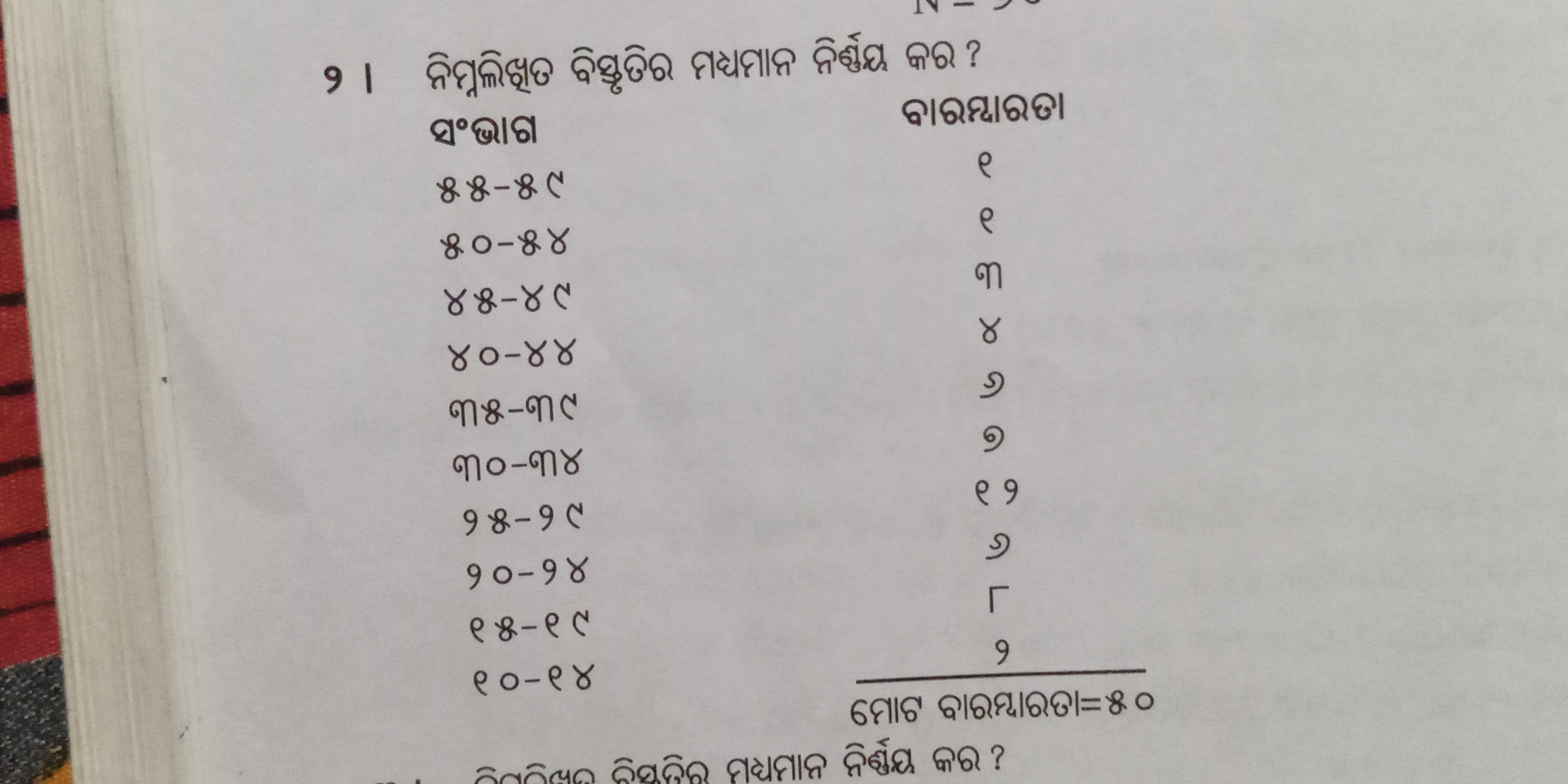
ନିମ୍ନଲିଖିତ ବିସ୍ତୃତିର ମଧ୍ୟମାନ ନିର୍ଣ୍ଣୟ କର?
Understand the Problem
ଏହି ପ୍ରଶ୍ନରେ, ଆମକୁ ଏକ ବିତରଣର ମଧ୍ୟମାନ(median) ନିର୍ଣ୍ଣୟ କରିବାକୁ କୁହାଯାଉଛି। ଦିଆଯାଇଥିବା ତଥ୍ୟରୁ ମଧ୍ୟମାନ କିପରି ବାହାର କରାଯାଏ ତାହା ଏଠାରେ ଦର୍ଶାଯାଇଛି ।
Answer
$41.33$
Answer for screen readers
$41.33$
Steps to Solve
- ବାରମ୍ବାରତା ସାରଣୀ ସଜାନ୍ତୁ ଏବଂ ସଂଚୟୀ ବାରମ୍ବାରତା ଗଣନା କରନ୍ତୁ ଏହି ସମସ୍ୟାକୁ ସମାଧାନ କରିବା ପାଇଁ, ଆମକୁ ପ୍ରଥମେ ତଥ୍ୟକୁ ସଜାଇବାକୁ ପଡିବ ଏବଂ ସେମାନଙ୍କର ସଂଚୟୀ ବାରମ୍ବାରତା ଗଣନା କରିବାକୁ ପଡିବ। ଟେବୁଲ୍ ନିମ୍ନଲିଖିତ ଭାବରେ ସଜାଯାଇଛି:
| ସମ୍ଭାଗ | ବାରମ୍ବାରତା (f) | ସଂଚୟୀ ବାରମ୍ବାରତା (cf) |
|---|---|---|
| 10-14 | 1 | 1 |
| 20-24 | 1 | 2 |
| 30-34 | 4 | 6 |
| 34-38 | 7 | 13 |
| 38-40 | 9 | 22 |
| 40-44 | 9 | 31 |
| 44-48 | 9 | 40 |
| 48-52 | 6 | 46 |
| 52-56 | 4 | 50 |
-
ମଧ୍ୟମ ଶ୍ରେଣୀ ନିର୍ଣ୍ଣୟ କରନ୍ତୁ ମୋଟ ବାରମ୍ବାରତା ହେଉଛି $N = 50$. ମଧ୍ୟମାନ(median)ର ସ୍ଥିତି ହେଉଛି $\frac{N}{2} = \frac{50}{2} = 25$. ଏହା ଦର୍ଶାଉଛି ଯେ ମଧ୍ୟମାନ 25 ତମ ପର୍ଯ୍ୟବେକ୍ଷଣରେ ଅବସ୍ଥିତ। ସଂଚୟୀ ବାରମ୍ବାରତା ସାରଣୀରେ, 25 ତମ ପର୍ଯ୍ୟବେକ୍ଷଣ 40-44 ସହିତ ଅନୁରୂପ ଅଛି, ତେଣୁ ମଧ୍ୟମ ଶ୍ରେଣୀ ହେଉଛି 40-44।
-
ମଧ୍ୟମାନ ଗଣନା କରନ୍ତୁ ମଧ୍ୟମାନ ଗଣନା କରିବାକୁ, ଆମେ ନିମ୍ନଲିଖିତ ସୂତ୍ର ବ୍ୟବହାର କରିପାରିବା: $M = L + \left( \frac{\frac{N}{2} - cf}{f} \right) \times h$ ଏଠାରେ: $L$ = ମଧ୍ୟମ ଶ୍ରେଣୀର ତଳ ସୀମା = 40 $N$ = ମୋଟ ବାରମ୍ବାରତା = 50 $cf$ = ମଧ୍ୟମ ଶ୍ରେଣୀ ପୂର୍ବରୁ ସଂଚୟୀ ବାରମ୍ବାରତା = 22 $f$ = ମଧ୍ୟମ ଶ୍ରେଣୀର ବାରମ୍ବାରତା = 9 $h$ = ଶ୍ରେଣୀର ଆକାର = 4 (44 - 40)
ମୂଲ୍ୟଗୁଡିକ ଭର୍ତ୍ତି କରନ୍ତୁ:
$M = 40 + \left( \frac{25 - 22}{9} \right) \times 4$
$M = 40 + \left( \frac{3}{9} \right) \times 4$
$M = 40 + \frac{12}{9}$
$M = 40 + 1.33$
$M = 41.33$
ତେଣୁ, ଦିଆଯାଇଥିବା ତଥ୍ୟ ପାଇଁ ମଧ୍ୟମାନ ହେଉଛି 41.33।
$41.33$
More Information
ମଧ୍ୟମାନ ହେଉଛି ଏକ ଷ୍ଟାଟିଷ୍ଟିକାଲ୍ ମାପ ଯାହାକି ଏକ ଡାଟା ସେଟ୍ର ମଧ୍ୟଭାଗକୁ ସୂଚାଇଥାଏ। ଏହାର ଅର୍ଥ ହେଉଛି 50% ଡାଟା ପଏଣ୍ଟ ମଧ୍ୟମାନରୁ କମ୍ ଏବଂ ଅବଶିଷ୍ଟ 50% ଏହାଠାରୁ ଅଧିକ ଅଟେ।
Tips
- ଶ୍ରେଣୀର ଆକାରକୁ ଭୁଲ୍ ଭାବରେ ଗଣନା କରିବା।
- ମଧ୍ୟମ ଶ୍ରେଣୀ ଚିହ୍ନଟ କରିବାରେ ଭୁଲ୍ କରିବା।
- ସୂତ୍ରଗୁଡିକରେ ମୂଲ୍ୟକୁ ଭୁଲ୍ ଭାବରେ ପ୍ରତିସ୍ଥାପନ କରିବା।
AI-generated content may contain errors. Please verify critical information