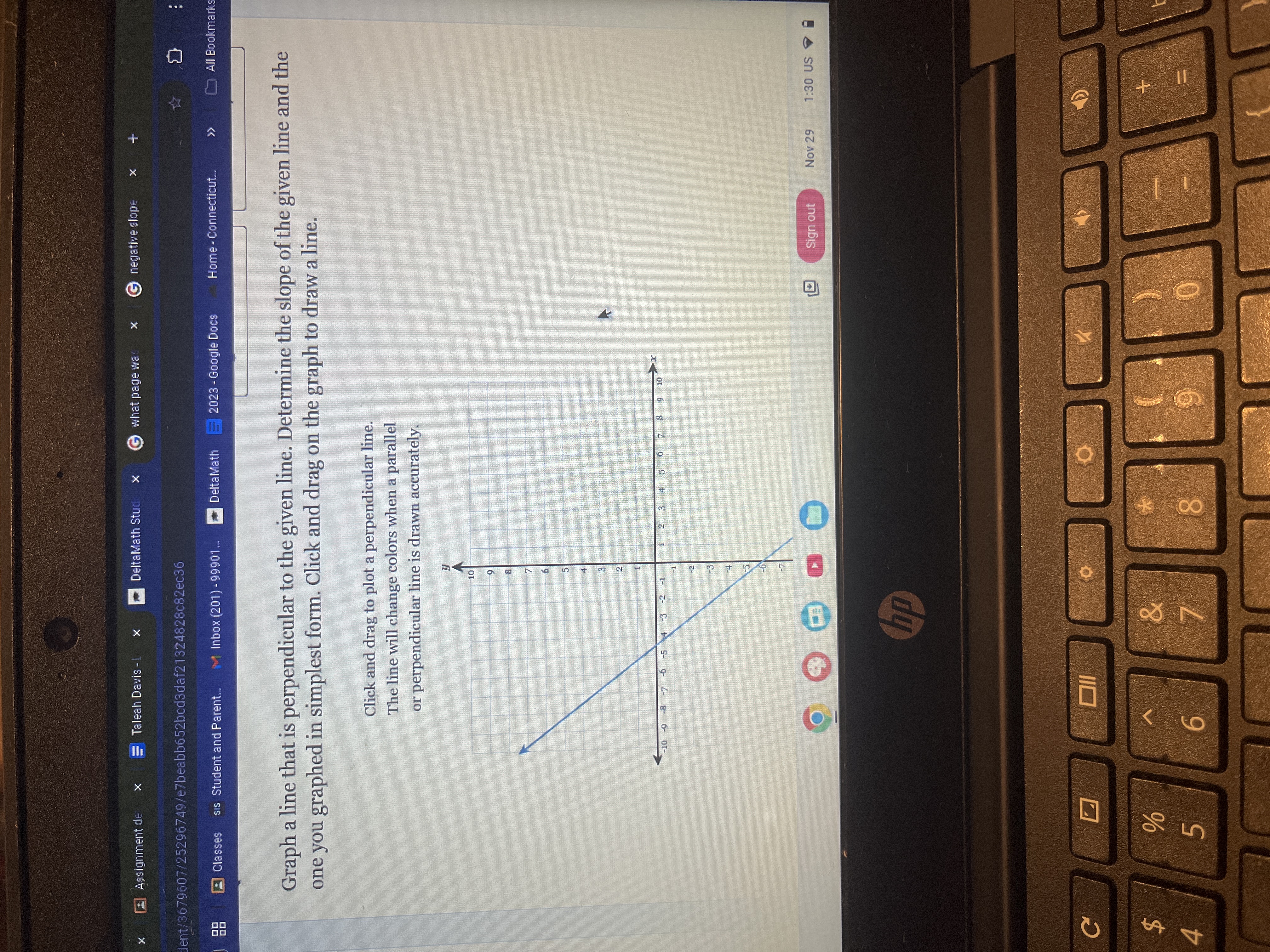
Graph a line that is perpendicular to the given line. Determine the slope of the given line and the one you graphed in simplest form.

Steps to Solve

1. Identify the slope of the given line

To find the slope of the given line, we need to use its endpoints or its equation. From the graph, we can see that the line has a negative slope. If we select two points on this line, say (0, 3) and (5, -2), we can calculate the slope using the formula:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Substituting the coordinates into the formula gives:

$$ m = \frac{-2 - 3}{5 - 0} = \frac{-5}{5} = -1 $$

So, the slope of the given line is $m = -1$.

2. Determine the slope of the perpendicular line

The slope of a line that is perpendicular to another is the negative reciprocal of the original line's slope. Since the slope of the given line is $-1$, the perpendicular slope $m_{\perp}$ is:

$$ m_{\perp} = -\frac{1}{m} = -\frac{1}{-1} = 1 $$

Thus, the slope of the perpendicular line is $m_{\perp} = 1$.

3. Graph the perpendicular line

To graph the line with slope $1$, start from a point on the original line. For example, we can use the point (0, 3). Using the slope, rise 1 unit and run 1 unit to the right. Plot another point at (1, 4). Connect these points to form the perpendicular line.