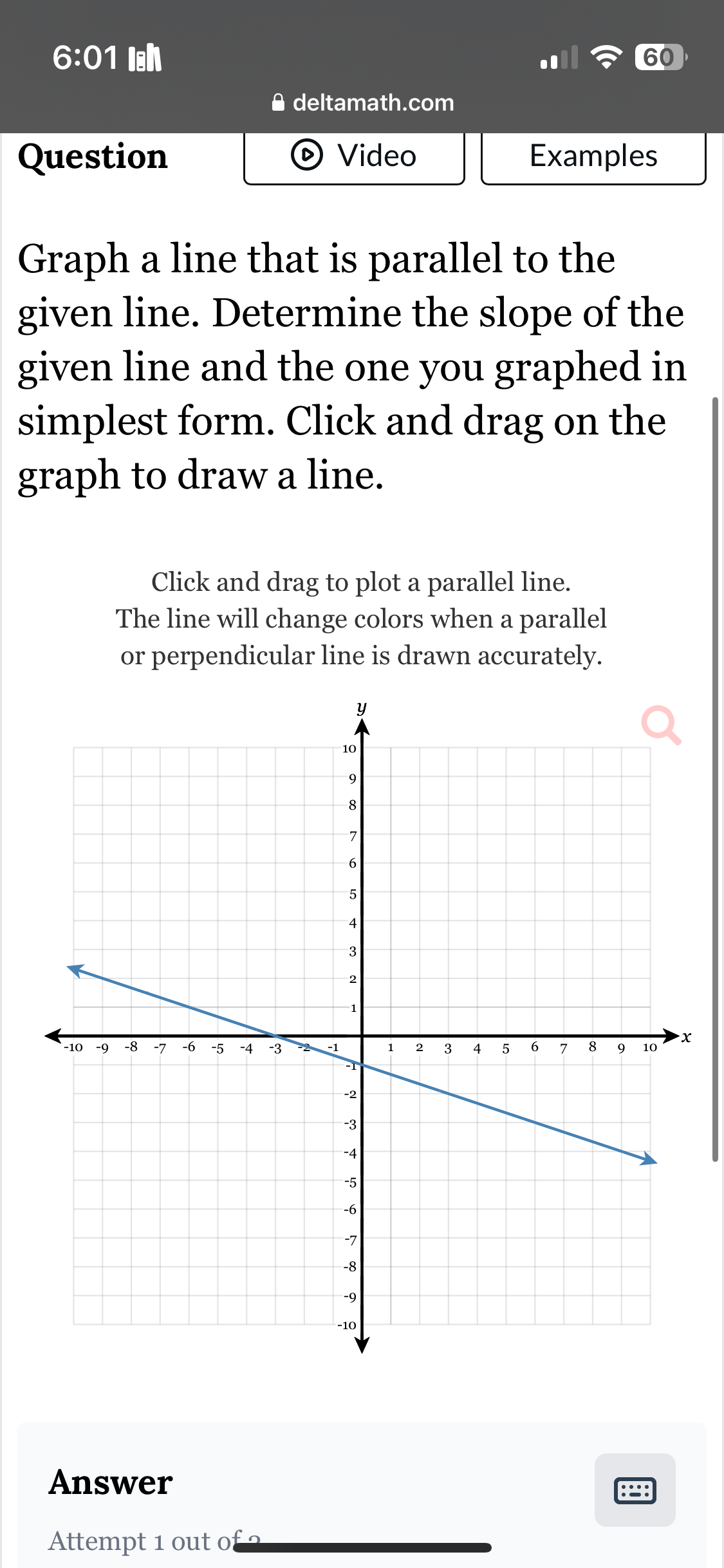
Graph a line that is parallel to the given line. Determine the slope of the given line and the one you graphed in simplest form.

Steps to Solve

1. Identify the slope of the given line

First, we need to determine the slope of the given line. The slope ( m ) can often be identified from the graph. If the line moves downwards from left to right, the slope is negative.

2. Finding the slope

To get the slope from two points on the line, use the formula:

$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

Choose two clear points from the graph (e.g., ((-1, 3)) and ((2, -2))). The slope calculation will be:

$$ m = \frac{-2 - 3}{2 - (-1)} = \frac{-5}{3} $$

3. Determine the slope of the parallel line

Since parallel lines have the same slope, the slope of the new line will also be ( m = -\frac{5}{3} ).

4. Graph the new line

Using the slope ( m = -\frac{5}{3} ), you can graph the parallel line. Start from any point you choose, e.g., (0, b) where ( b ) is the y-intercept of your chosen point.

5. Plotting the line

From your chosen point, move 3 units right (positive x-direction) and 5 units down (negative y-direction), or 3 units left and 5 units up, to find another point on your parallel line.