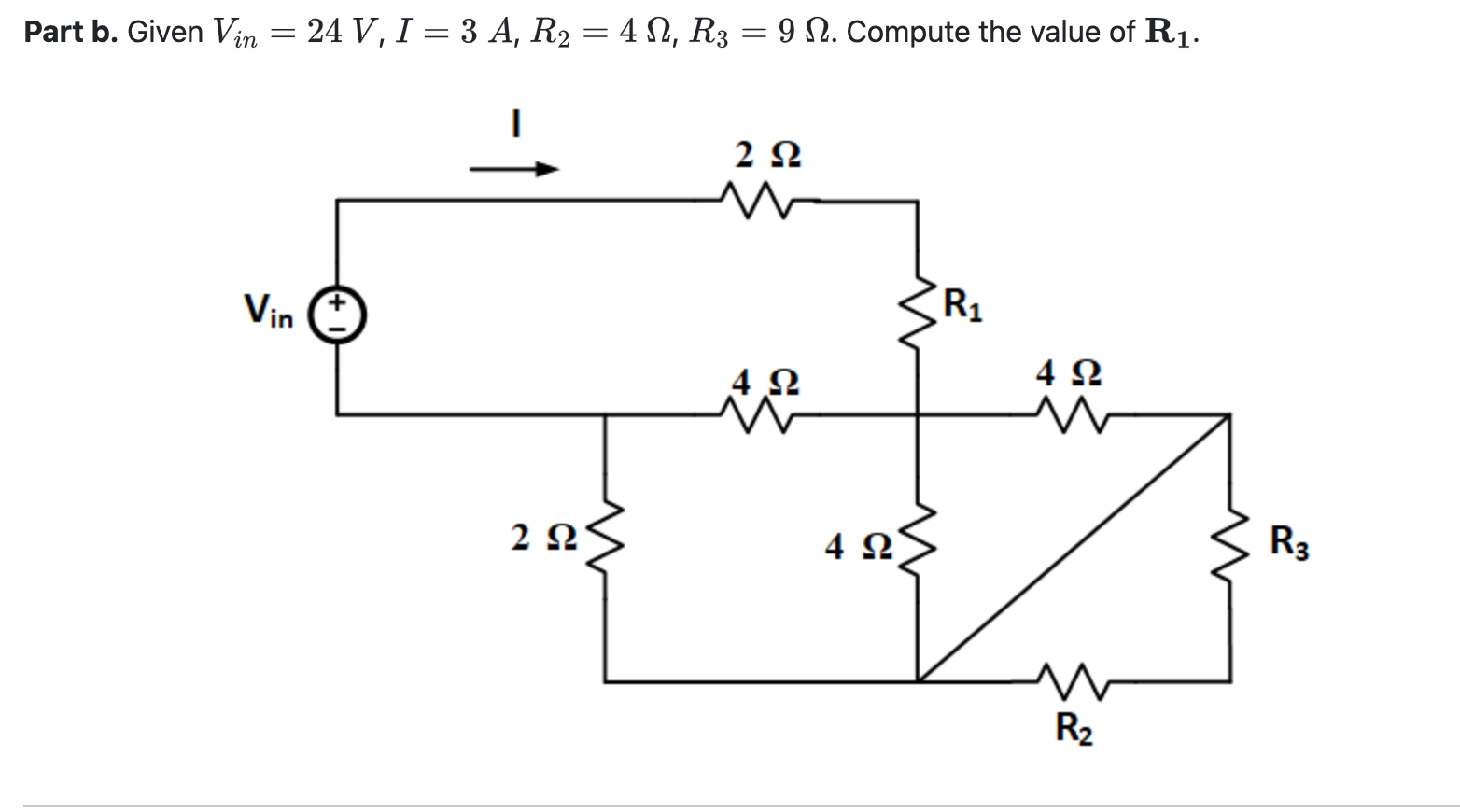
Given $V_{in} = 24V$, $I = 3A$, $R_2 = 4\Omega$, $R_3 = 9\Omega$, compute the value of $R_1$ in the circuit.

Steps to Solve

1. Simplify the resistor network.

Notice that the $4\Omega$ resistor, $R_2 = 4\Omega$, $R_3 = 9\Omega $ and the remaining $4\Omega$ resistor form a Wheatstone bridge. Since $4\Omega / 4\Omega \ne 4\Omega / 9\Omega$, the bridge is unbalanced, and we sadly can't simplify it to two series resistors in parallel. Also notice that the $4\Omega$ resistor that is in series with the $4\Omega$ resistor that is in parallel with $R_2 = 4\Omega$ does nothing, since it is shorted out. Thus, the effective resistance is zero.

2. Redraw the simplified circuit.

After the simplification, we have a $2\Omega$ resistor in series with $R_1$, which is in parallel with the series combination of a $2\Omega$ resistor and $R_3 = 9\Omega$. $R_2 = 4\Omega$ is in parallel with $R_3 = 9 \Omega$. Furthermore, the simplified $4\Omega$ resistor is parallel to $R_2 = 4\Omega$, so they can be combined using the parallel resistor formula.

3. Calculate the equivalent resistance of $R_2$ and $4\Omega$

Since they are in parallel, we use the formula for resistors in parallel. Let $R_{2,4}$ be the equivalent resistance. $$ R_{2,4} = \frac{R_2 \cdot 4}{R_2 + 4} = \frac{4 \cdot 4}{4 + 4} = \frac{16}{8} = 2\Omega$$

4. Calculate the equivalent resistance of $R_3$ and $R_{2, 4}$.

Since $R_3$ and $R_{2,4}$ are in parallel, we combine them into $R_{3,2,4}$: $$ R_{3,2,4} = \frac{R_3 \cdot R_{2,4}}{R_3 + R_{2,4}} = \frac{9 \cdot 2}{9 + 2} = \frac{18}{11}\Omega$$

5. Calculate the equivalent series resistance.

The $2\Omega$ resistor at the bottom of the circuit is in series with the parallel combination we just computed. Let's call this combined resistance $R_b$, where the 'b' stands for bottom.

$$R_b = 2 + \frac{18}{11} = \frac{22 + 18}{11} = \frac{40}{11}\Omega$$

6. Label the $2\Omega$ resistor at the top as $R_t$ for top.

7. Calculate the total equivalent resistance $R_{eq}$.

We know that the total current $I$ is 3A and the input voltage $V_{in}$ is 24V. Therefore, using Ohm's Law, the equivalent resistance is: $$R_{eq} = \frac {V_{in}}{I} = \frac{24}{3} = 8\Omega$$

8. Calculate the equivalent resistance of $R_1$ and $R_t$.

The equivalent resistance of the circuit is the parallel combination of ($R_t$ + $R_1$) and $R_b$. Let $R_{t1}$ be the equivalent

$$R_{t1} = R_t + R_1 = 2 + R_1$$

9. Calculate $R_1$.

We are given $R_{eq} = 8\Omega$, so $$R_{eq} = \frac{R_b \cdot R_{t1}}{R_b + R_{t1}}$$ $$8 = \frac{\frac{40}{11} \cdot (2 + R_1)}{\frac{40}{11} + (2 + R_1)}$$ $$8 \cdot (\frac{40}{11} + 2 + R_1) = \frac{40}{11} \cdot (2 + R_1)$$ $$8 \cdot (\frac{40}{11} + \frac{22}{11} + R_1) = \frac{80}{11} + \frac{40}{11}R_1$$ $$8 \cdot (\frac{62}{11} + R_1) = \frac{80}{11} + \frac{40}{11}R_1$$ $$\frac{496}{11} + 8R_1 = \frac{80}{11} + \frac{40}{11}R_1$$ $$8R_1 - \frac{40}{11}R_1 = \frac{80}{11} - \frac{496}{11}$$ $$\frac{88 - 40}{11}R_1 = \frac{-416}{11}$$ $$\frac{48}{11}R_1 = \frac{-416}{11}$$ $$R_1 = \frac{-416}{48} = \frac{-208}{24} = \frac{-104}{12} = \frac{-52}{6} = \frac{-26}{3} \approx -8.666$$ Therefore, $R_1 \approx -8.666$.