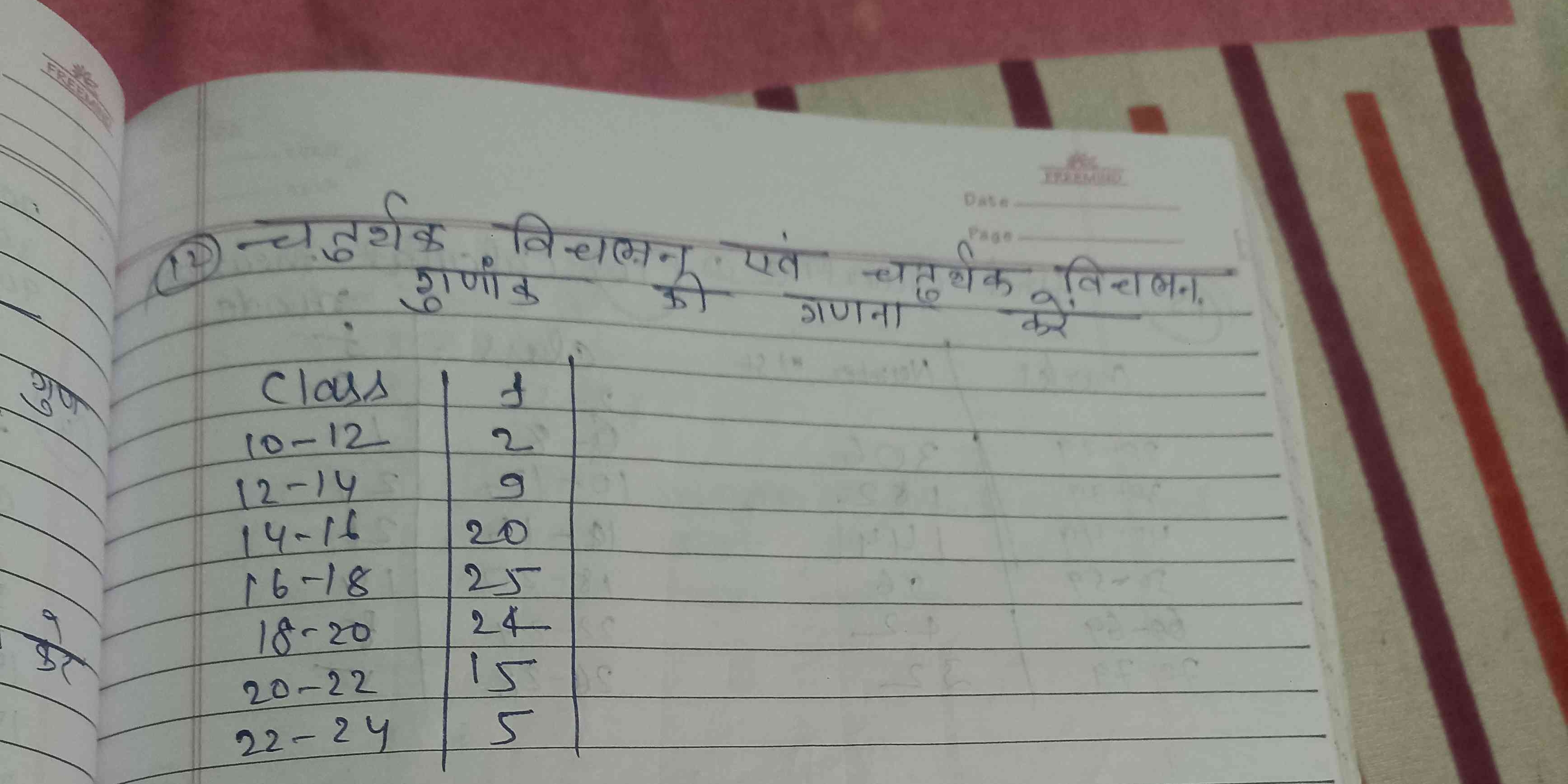
चclass के लिए चतुर्थक विचलन और चतुर्थक विचलन के गुणांक की गणना करें: class 10-12 (frequency 2), 12-14 (frequency 9), 14-16 (frequency 20), 16-18 (frequency 25), 18-20 (frequency 24... चclass के लिए चतुर्थक विचलन और चतुर्थक विचलन के गुणांक की गणना करें: class 10-12 (frequency 2), 12-14 (frequency 9), 14-16 (frequency 20), 16-18 (frequency 25), 18-20 (frequency 24), 20-22 (frequency 15), 22-24 (frequency 5).
Understand the Problem
यह प्रश्न चतुर्थक विचलन और चतुर्थक विचलन के गुणांक की गणना करने के लिए कह रहा है। इसके लिए, हमें दिए गए डेटा के लिए चतुर्थक सीमाओं (Q1 और Q3) का पता लगाना होगा, फिर चतुर्थक विचलन और अंत में चतुर्थक विचलन के गुणांक की गणना करनी होगी।
Answer
चतुर्थक विचलन $= 2.0915$ चतुर्थक विचलन का गुणांक $= 0.11957$
Answer for screen readers
चतुर्थक विचलन $QD = 2.0915$ चतुर्थक विचलन का गुणांक $= 0.11957$
Steps to Solve
- संचयी बारंबारता (Cumulative Frequency) सारणी बनाइए
संचयी बारंबारता का उपयोग चतुर्थक सीमाओं की पहचान करने के लिए किया जाता है।
| Class | Frequency (f) | Cumulative Frequency (cf) |
|---|---|---|
| 10-12 | 2 | 2 |
| 12-14 | 9 | 11 |
| 14-16 | 20 | 31 |
| 16-18 | 25 | 56 |
| 18-20 | 24 | 80 |
| 20-22 | 15 | 95 |
| 22-24 | 5 | 100 |
- प्रथम चतुर्थक $Q_1$ ज्ञात कीजिए
$Q_1$ की गणना करने के लिए, हमें पहले $N/4$ की स्थिति ज्ञात करनी होगी, जहाँ N कुल बारंबारता है, और फिर $Q_1$ के वर्ग की पहचान करनी होगी।
$N = 100$, इसलिए $N/4 = 100/4 = 25$.
संचयी बारंबारता सारणी में, 25, 31 में निहित है, इसलिए $Q_1$ वर्ग 14-16 है।
सूत्र का उपयोग करें: $$Q_1 = L + \frac{\frac{N}{4} - cf}{f} \times h$$
जहां: $L$ = $Q_1$ वर्ग की निचली सीमा = 14 $cf$ = $Q_1$ वर्ग से पहले वर्ग की संचयी बारंबारता = 11 $f$ = $Q_1$ वर्ग की बारंबारता = 20 $h$ = वर्ग आकार = 2
अतः, $$Q_1 = 14 + \frac{25 - 11}{20} \times 2 = 14 + \frac{14}{20} \times 2 = 14 + 1.4 = 15.4$$
- तृतीय चतुर्थक $Q_3$ ज्ञात कीजिए
$Q_3$ की गणना करने के लिए, पहले $3N/4$ की स्थिति ज्ञात करें, जहाँ $N$ कुल बारंबारता है, और फिर $Q_3$ के वर्ग की पहचान करें।
$N = 100$, इसलिए $3N/4 = 3 \times 100/4 = 75$.
संचयी बारंबारता सारणी में, 75, 80 निहित है, इसलिए $Q_3$ वर्ग 18-20 है।
सूत्र का उपयोग करें: $$Q_3 = L + \frac{\frac{3N}{4} - cf}{f} \times h$$
जहां: $L$ = $Q_3$ वर्ग की निचली सीमा = 18 $cf$ = $Q_3$ वर्ग से पहले वर्ग की संचयी बारंबारता = 56 $f$ = $Q_3$ वर्ग की बारंबारता = 24 $h$ = वर्ग आकार = 2
अतः, $$Q_3 = 18 + \frac{75 - 56}{24} \times 2 = 18 + \frac{19}{24} \times 2 = 18 + 1.583 = 19.583$$
- चतुर्थक विचलन ज्ञात कीजिए
चतुर्थक विचलन (QD) की गणना निम्न सूत्र का उपयोग करके की जाती है:
$$QD = \frac{Q_3 - Q_1}{2}$$ $Q_1 = 15.4$ $Q_3 = 19.583$
$$QD = \frac{19.583 - 15.4}{2} = \frac{4.183}{2} = 2.0915$$
- चतुर्थक विचलन का गुणांक ज्ञात कीजिए
चतुर्थक विचलन के गुणांक की गणना निम्न सूत्र का उपयोग करके की जाती है:
$$\text{Coefficient of QD} = \frac{Q_3 - Q_1}{Q_3 + Q_1}$$
$$= \frac{19.583 - 15.4}{19.583 + 15.4} = \frac{4.183}{34.983} = 0.11957$$
चतुर्थक विचलन $QD = 2.0915$ चतुर्थक विचलन का गुणांक $= 0.11957$
More Information
चतुर्थक विचलन, आंकड़ों के प्रसार को समझने में मदद करता है, जबकि इसका गुणांक हमें दो अलग-अलग डेटासेट के प्रसार की तुलना करने की अनुमति देता है। इसे सापेक्ष प्रसार का माप माना जाता है।
Tips
- संचयी बारंबारता की गणना करते समय त्रुटियां।
- $Q_1$ और $Q_3$ के सही वर्गों की पहचान करने में गलतियाँ।
- सूत्रों में गलत मानों का उपयोग करना।
- अंतिम उत्तर को गोल करने में त्रुटियाँ।
AI-generated content may contain errors. Please verify critical information