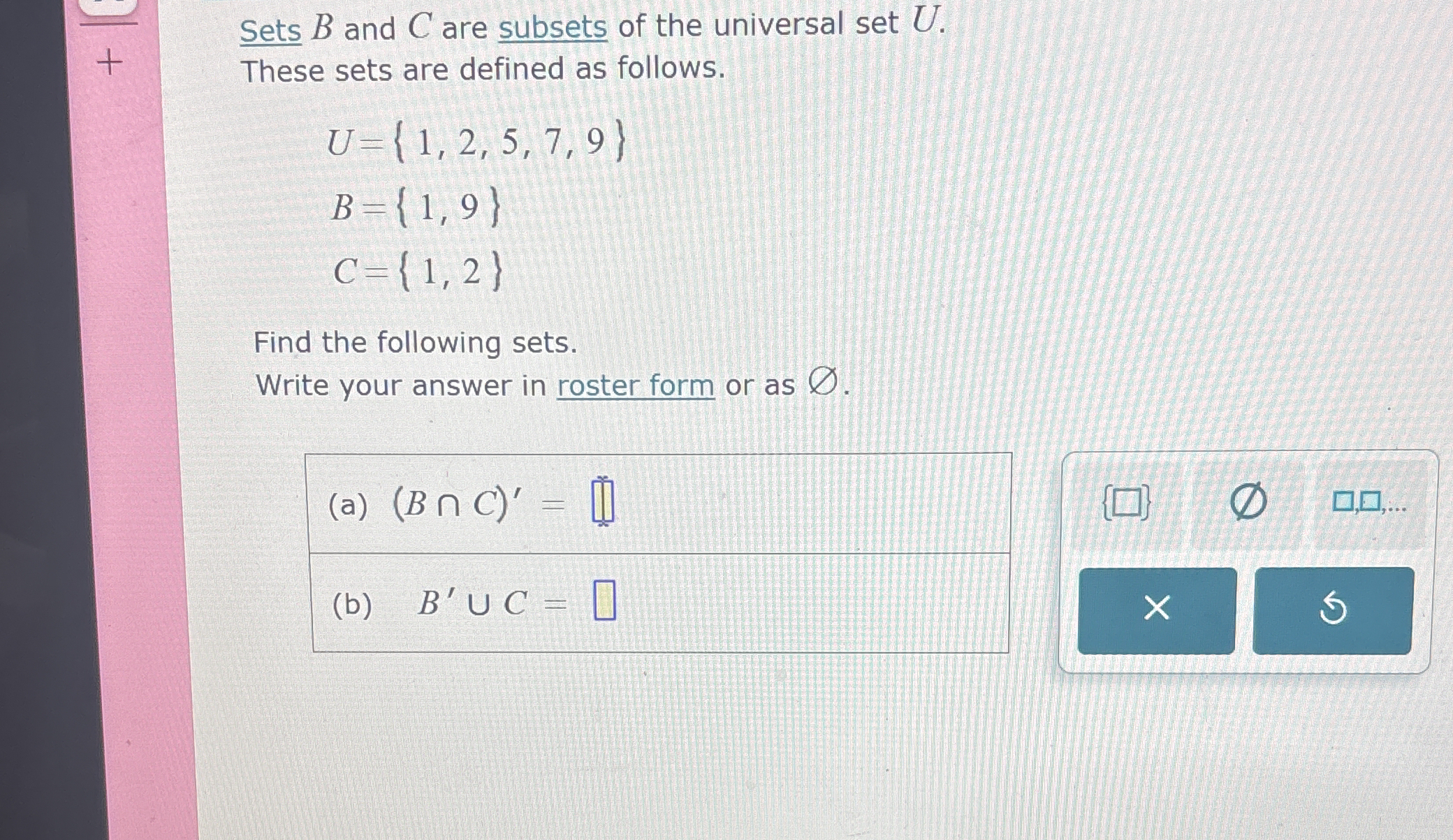
Given the sets U = {1, 2, 5, 7, 9}, B = {1, 9}, and C = {1, 2}, find: (a) (B ∩ C)' (b) B' ∪ C
Understand the Problem
The question involves set theory and asks to find the result of two set operations. In part (a), it asks to find the complement of the intersection of sets B and C, denoted as (B ∩ C)'. In part (b), it asks to find the union of the complement of set B and set C, denoted as B' ∪ C. The sets are defined as follows: U = {1, 2, 5, 7, 9}, B = {1, 9}, and C = {1, 2}.
Answer
(a) $(B \cap C)' = \{2, 5, 7, 9\}$ (b) $B' \cup C = \{1, 2, 5, 7\}$
Answer for screen readers
(a) $(B \cap C)' = {2, 5, 7, 9}$ (b) $B' \cup C = {1, 2, 5, 7}$
Steps to Solve
- Find the intersection of B and C
$B \cap C$ means the elements that are in both B and C. $B = {1, 9}$ and $C = {1, 2}$, so $B \cap C = {1}$. 2. Find the complement of $B \cap C$
$(B \cap C)'$ means all the elements in U that are not in $B \cap C$. Since $B \cap C = {1}$ and $U = {1, 2, 5, 7, 9}$, then $(B \cap C)' = {2, 5, 7, 9}$. 3. Find the complement of B
$B'$ means all the elements in U that are not in B. Since $B = {1, 9}$ and $U = {1, 2, 5, 7, 9}$, then $B' = {2, 5, 7}$. 4. Find the union of $B'$ and C
$B' \cup C$ means all the elements that are in $B'$ or C or both. Since $B' = {2, 5, 7}$ and $C = {1, 2}$, then $B' \cup C = {1, 2, 5, 7}$.
(a) $(B \cap C)' = {2, 5, 7, 9}$ (b) $B' \cup C = {1, 2, 5, 7}$
More Information
Set theory is a fundamental concept in mathematics that deals with the study of sets, which are collections of objects. The complement of a set A, denoted A', consists of all elements in the universal set U that are not in A. The intersection of two sets A and B, denoted $A \cap B$, consists of all elements that are in both A and B. The union of two sets A and B, denoted $A \cup B$, consists of all elements that are in A or B or both.
Tips
A common mistake is confusing intersection with union, or forgetting to consider the universal set when finding the complement. Another mistake is incorrectly listing the elements when determining the intersection, union, or complement of sets.
AI-generated content may contain errors. Please verify critical information