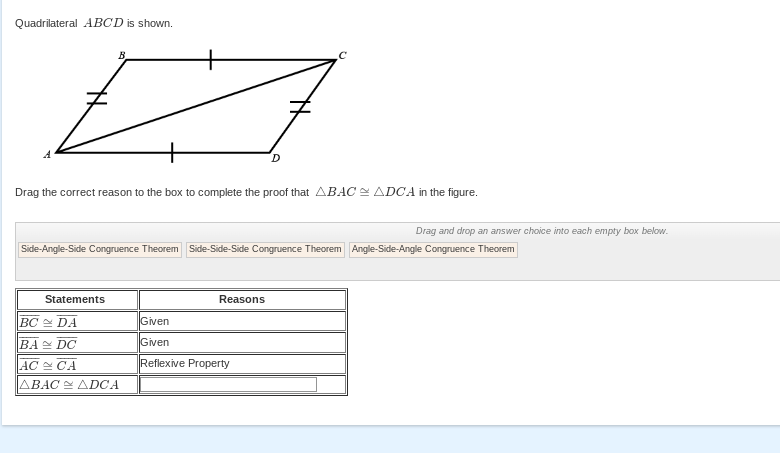
Given quadrilateral ABCD with certain sides and angles, complete the proof that triangle BAC is congruent to triangle DCA.
Understand the Problem
The question is asking to complete a proof showing that the triangles BAC and DCA are congruent using given congruences and appropriate theorems.
Answer
$\triangle BAC \cong \triangle DCA$
Answer for screen readers
$\triangle BAC \cong \triangle DCA$
Steps to Solve
- Identify Given Information
The problem states that segments $BC \cong DA$ and $BA \cong DC$, which are given as congruent sides of triangles $BAC$ and $DCA$.
- Use Reflexive Property
The segment $AC$ is common to both triangles $BAC$ and $DCA$, so we can state that $AC \cong CA$ by the reflexive property.
- Apply the Side-Side-Side Congruence Theorem
Since we have established that:
- $BC \cong DA$
- $BA \cong DC$
- $AC \cong CA$
We can use the Side-Side-Side (SSS) Congruence Theorem, which states that if the three sides of one triangle are congruent to the three sides of another triangle, then the triangles are congruent.
- Conclude Triangle Congruence
Thus, it follows that $\triangle BAC \cong \triangle DCA$ by the SSS Congruence Theorem.
$\triangle BAC \cong \triangle DCA$
More Information
This proof relies on understanding triangle congruence theorems, specifically the Side-Side-Side Congruence Theorem. The congruence relationships and the reflexive property are crucial in establishing triangle congruence.
Tips
- Confusing the properties of congruence (e.g., reflexive vs. symmetric).
- Not clearly stating the reasons for congruences.
AI-generated content may contain errors. Please verify critical information