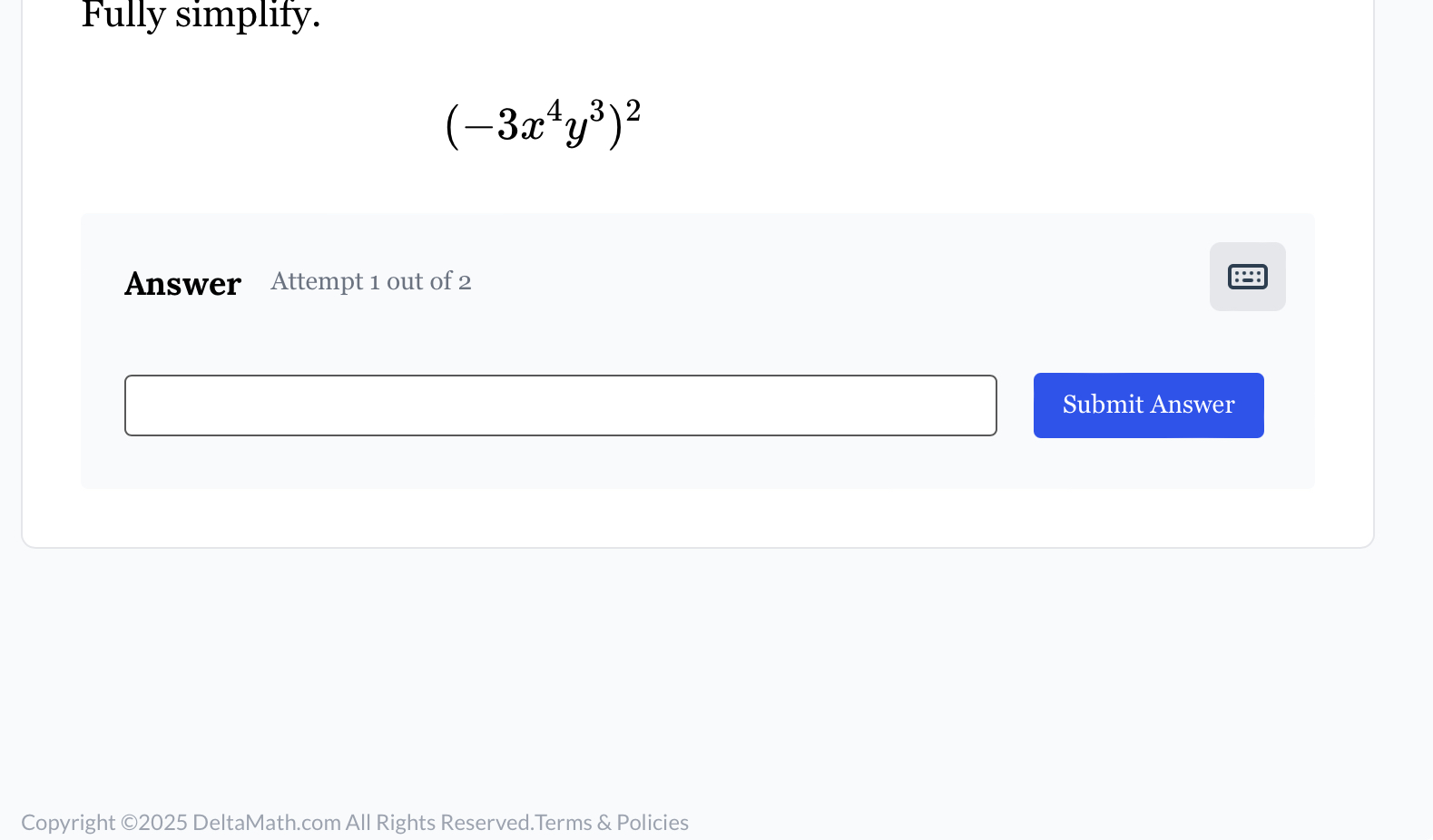
Fully simplify (−3x^4y^3)^2.
Understand the Problem
The question is asking us to fully simplify the expression (-3x^4y^3)^2. This involves applying the power of a product and simplifying the resulting terms.
Answer
$9x^8y^6$
Answer for screen readers
The fully simplified expression is $9x^8y^6$.
Steps to Solve
-
Apply the power of a product rule To simplify the expression, we apply the power of a product rule, which states that $(ab)^n = a^n b^n$. We have: $$ (-3x^4y^3)^2 = (-3)^2 (x^4)^2 (y^3)^2 $$
-
Calculate each component Now, calculate each term individually:
- $(-3)^2 = 9$
- $(x^4)^2 = x^{4 \cdot 2} = x^8$
- $(y^3)^2 = y^{3 \cdot 2} = y^6$
- Combine the results Now combine the results from the previous calculation: $$ (-3x^4y^3)^2 = 9x^8y^6 $$
The fully simplified expression is $9x^8y^6$.
More Information
This simplification demonstrates how powers apply to both coefficients and variables within an expression. The power of a product rule is essential in expanding and simplifying algebraic expressions.
Tips
- A common mistake is forgetting to square the negative sign, which can lead to getting $-9x^8y^6$ instead of the correct positive value $9x^8y^6$.
- Another mistake is misapplying the power rule, for example, writing $(x^4)^2 = x^6$ instead of $x^8$.
AI-generated content may contain errors. Please verify critical information