Fully simplify 15x^2y^2 / 25xy^7 using only positive exponents.
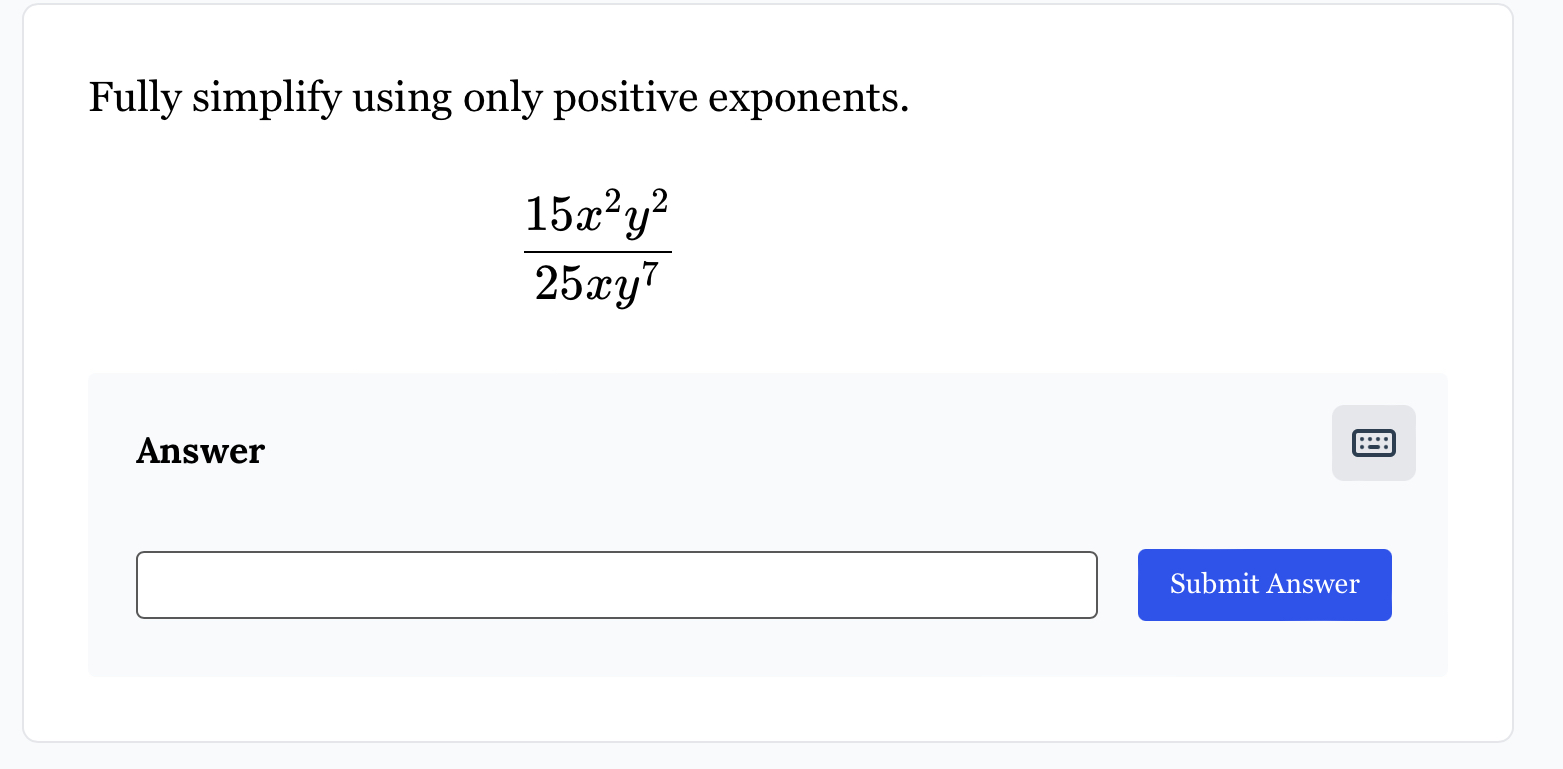
Understand the Problem
The question is asking to simplify the expression \( \frac{15x^{2}y^{2}}{25xy^{7}} \) using only positive exponents, which involves factoring and reducing the fractions.
Answer
The simplified expression is $$ \frac{3x}{5y^5} $$
Answer for screen readers
The fully simplified expression is $$ \frac{3x}{5y^5} $$
Steps to Solve
-
Factor the Coefficients The coefficients 15 and 25 can be factored. Divide both by their greatest common factor (GCF), which is 5. $$ \frac{15}{25} = \frac{3}{5} $$
-
Simplify the Variables For the variables, simplify (x^2) and (x): $$ \frac{x^2}{x} = x^{2-1} = x^1 = x $$
-
Simplify the y Terms For the (y) terms, simplify (y^2) and (y^7): $$ \frac{y^2}{y^7} = y^{2-7} = y^{-5} $$
-
Combine the Results Now combine everything: $$ \frac{3x}{5y^{5}} $$
-
Rewrite with Positive Exponents Rewrite (y^{-5}) to ensure all exponents are positive: $$ = \frac{3x}{5y^5} $$
The fully simplified expression is $$ \frac{3x}{5y^5} $$
More Information
This simplification process utilizes the properties of exponents and factors out the greatest common factors in both the coefficients and the variables. It's essential when simplifying fractions that involve variables with exponents.
Tips
- Forgetting to factor out the greatest common factor (GCF) for the coefficients.
- Not applying the laws of exponents correctly when simplifying variables.
- Leaving the result with negative exponents instead of converting them to positive.
AI-generated content may contain errors. Please verify critical information