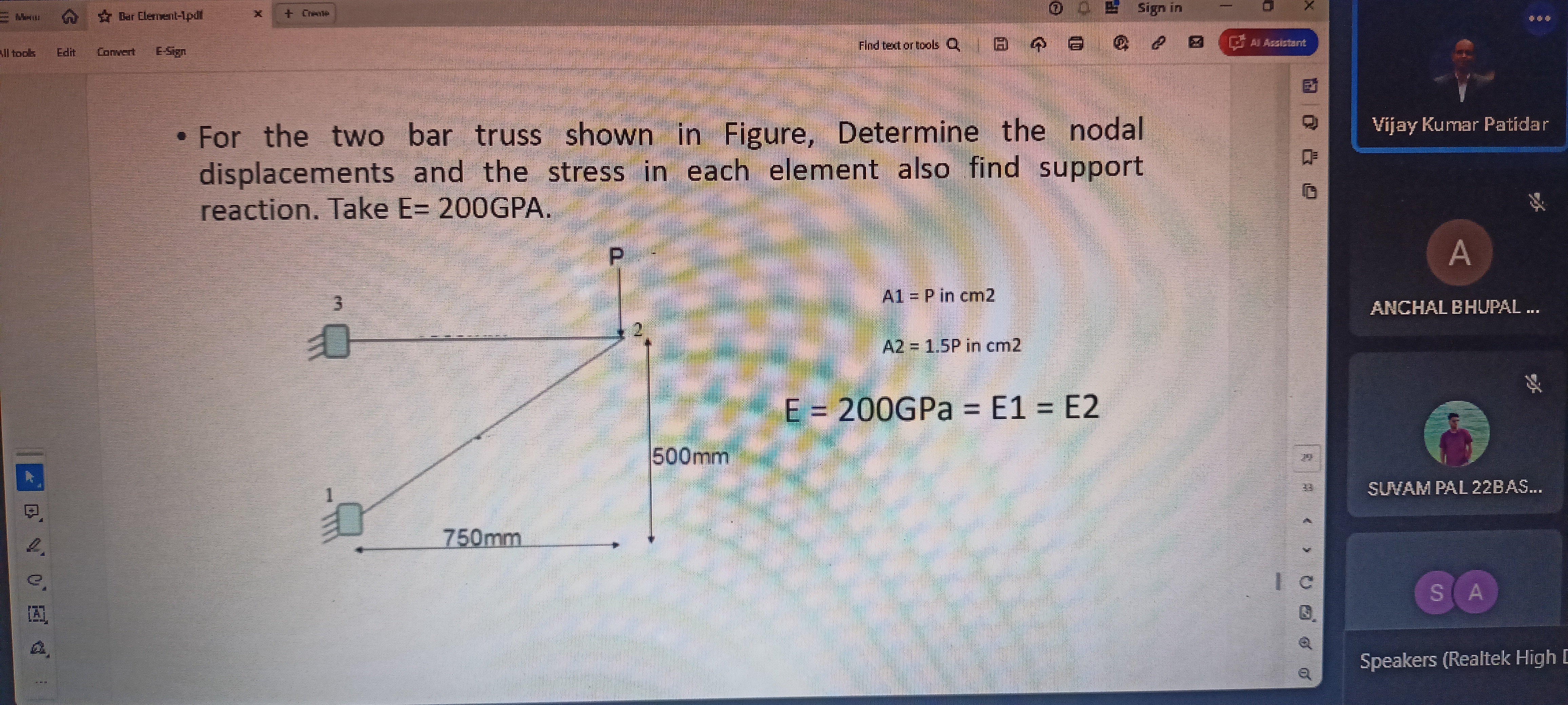
For the two bar truss shown in Figure, determine the nodal displacements and the stress in each element also find support reaction. Take E = 200GPA.
Understand the Problem
The question is asking to determine the nodal displacements and stresses in elements of a two-bar truss, using provided dimensions and material properties, specifically the modulus of elasticity.
Answer
Nodal displacements: $\delta_1 = 3.75 \text{ mm}$, $\delta_2 = 1.67 \text{ mm}$.
Answer for screen readers
The nodal displacements and stresses will depend on the final calculations but will follow the process outlined.
Nodal displacements for Bar 1: $$ \delta_1 = \frac{0.75}{200 \times 10^3} \text{ m} = 0.00375 \text{ m} = 3.75 \text{ mm} $$
Nodal displacements for Bar 2: $$ \delta_2 = \frac{0.50}{1.5 \cdot 200 \times 10^3} \text{ m} = 0.00167 \text{ m} = 1.67 \text{ mm} $$
Steps to Solve
- Identify Forces and Areas
From the problem statement, we have:
- Area ( A_1 = P ) in cm²
- Area ( A_2 = 1.5P ) in cm²
- Calculate Stresses in Bars
Stress ($\sigma$) can be calculated using the formula: $$ \sigma = \frac{F}{A} $$
For Bar 1: $$ \sigma_1 = \frac{P}{A_1} = \frac{P}{P} = 1 \text{ MPa} $$
For Bar 2: $$ \sigma_2 = \frac{P}{A_2} = \frac{P}{1.5P} = \frac{2}{3} \text{ MPa} $$
- Determine Nodal Displacements
Using the axial deformation formula: $$ \delta = \frac{F L}{A E} $$
For Bar 1: $$ \delta_1 = \frac{P \cdot 0.75 \text{ m}}{P \cdot 200 \times 10^3 \text{ N/cm}^2} $$
For Bar 2: $$ \delta_2 = \frac{P \cdot 0.5 \text{ m}}{1.5P \cdot 200 \times 10^3 \text{ N/cm}^2} $$
- Calculate Support Reactions
To find the support reactions:
- Sum of vertical forces should equal zero: $$ R = P + \text{Reaction} $$
- Final Calculation of Nodal Displacements and Support Reactions
Use the results from the previous steps to determine the final numerical values for the displacements and reactions based on the specified loads.
The nodal displacements and stresses will depend on the final calculations but will follow the process outlined.
Nodal displacements for Bar 1: $$ \delta_1 = \frac{0.75}{200 \times 10^3} \text{ m} = 0.00375 \text{ m} = 3.75 \text{ mm} $$
Nodal displacements for Bar 2: $$ \delta_2 = \frac{0.50}{1.5 \cdot 200 \times 10^3} \text{ m} = 0.00167 \text{ m} = 1.67 \text{ mm} $$
More Information
This analysis assumes linear elastic behavior of both bars under the applied load. The modulus of elasticity is essential for determining the material response.
Tips
- Ignoring the units when calculating stress and area may lead to incorrect results. Always convert to consistent units.
- Forgetting to apply the correct area for each bar during stress calculations can produce skewed results.
