If \(\lim_{x \to 0} \frac{f(x)}{x} = 1\) and \(\lim_{x \to 0} g(x)\) exists and is nonzero, then evaluate each limit: a. \(\lim_{x \to 0} f(x)\) b. \(\lim_{x \to 0} \frac{f(x)}{g(x... If \(\lim_{x \to 0} \frac{f(x)}{x} = 1\) and \(\lim_{x \to 0} g(x)\) exists and is nonzero, then evaluate each limit: a. \(\lim_{x \to 0} f(x)\) b. \(\lim_{x \to 0} \frac{f(x)}{g(x)}\)
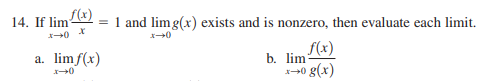
Understand the Problem
The question is asking to evaluate two limits given that (\lim_{x \to 0} \frac{f(x)}{x} = 1) and (\lim_{x \to 0} g(x)) exists and is nonzero. Part (a) asks for (\lim_{x \to 0} f(x)) and part (b) asks for (\lim_{x \to 0} \frac{f(x)}{g(x)}).
Answer
a. $0$ b. $0$
Answer for screen readers
a. $\lim_{x\to 0} f(x) = 0$ b. $\lim_{x\to 0} \frac{f(x)}{g(x)} = 0$
Steps to Solve
- Evaluate $\lim_{x\to 0} f(x)$
We are given that $\lim_{x\to 0} \frac{f(x)}{x} = 1$. We can rewrite $f(x)$ as $\frac{f(x)}{x} \cdot x$. Then, we can find the limit of $f(x)$ as $x$ approaches $0$: $$ \lim_{x\to 0} f(x) = \lim_{x\to 0} \left(\frac{f(x)}{x} \cdot x\right) $$ Using the limit product rule, we have: $$ \lim_{x\to 0} f(x) = \lim_{x\to 0} \frac{f(x)}{x} \cdot \lim_{x\to 0} x $$ Since $\lim_{x\to 0} \frac{f(x)}{x} = 1$ and $\lim_{x\to 0} x = 0$, we get: $$ \lim_{x\to 0} f(x) = 1 \cdot 0 = 0 $$
- Evaluate $\lim_{x\to 0} \frac{f(x)}{g(x)}$
We are given that $\lim_{x\to 0} g(x)$ exists and is nonzero, call it $L$, so $\lim_{x\to 0} g(x) = L \ne 0$. Also, we found that $\lim_{x\to 0} f(x) = 0$. We want to find $\lim_{x\to 0} \frac{f(x)}{g(x)}$. Using the limit quotient rule: $$ \lim_{x\to 0} \frac{f(x)}{g(x)} = \frac{\lim_{x\to 0} f(x)}{\lim_{x\to 0} g(x)} $$ Since $\lim_{x\to 0} f(x) = 0$ and $\lim_{x\to 0} g(x) = L$, where $L \ne 0$, we have: $$ \lim_{x\to 0} \frac{f(x)}{g(x)} = \frac{0}{L} = 0 $$
a. $\lim_{x\to 0} f(x) = 0$ b. $\lim_{x\to 0} \frac{f(x)}{g(x)} = 0$
More Information
The limit quotient rule is valid since $\lim_{x\to 0} g(x)$ exists and is nonzero.
Tips
A common mistake would be to assume that because $\lim_{x\to 0} \frac{f(x)}{x} = 1$, then $\lim_{x\to 0} f(x) = 1$ as well. However, multiplying by the limit of $x$ as $x \to 0$ gives the correct result. Another common mistake would be if $L = \lim_{x\to 0} g(x) = 0$, then $\lim_{x\to 0} \frac{f(x)}{g(x)}$ would be undefined but the problem says to assume that $L \ne 0$.
AI-generated content may contain errors. Please verify critical information