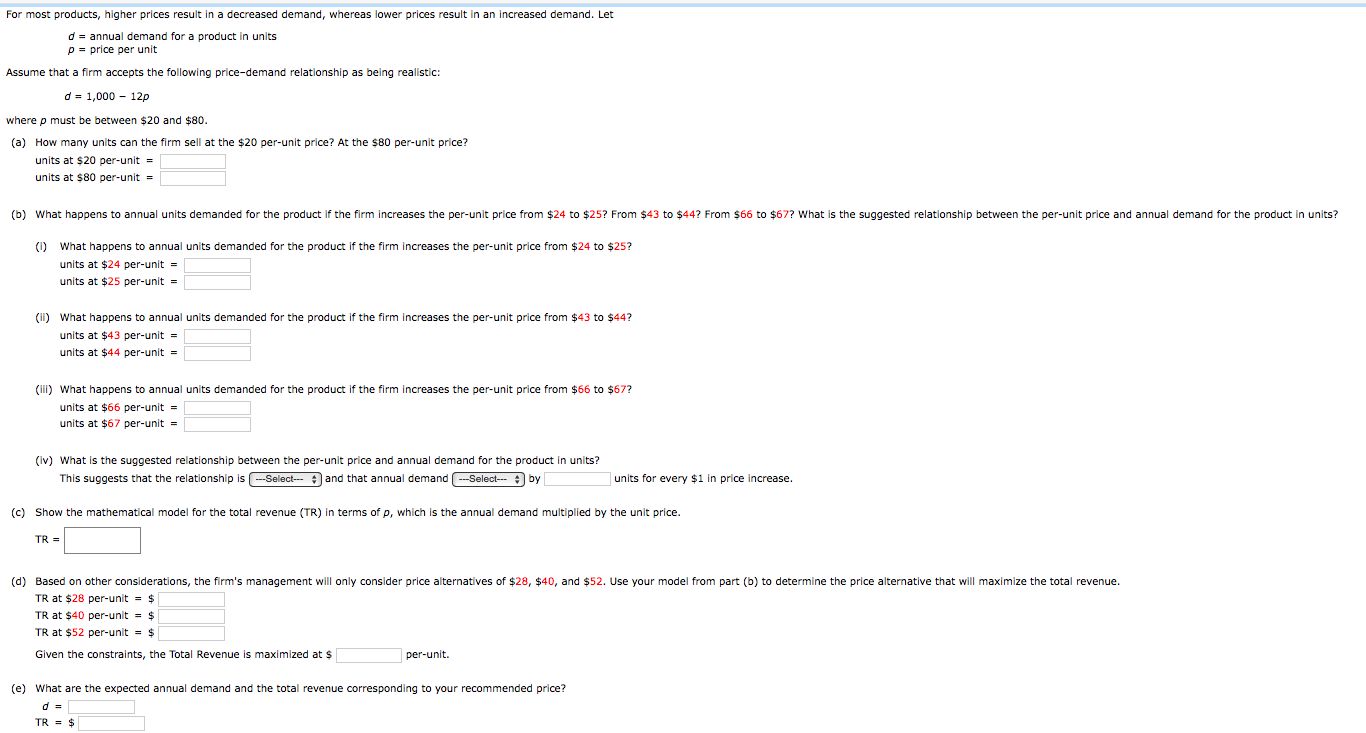
For most products, higher prices result in decreased demand, whereas lower prices result in increased demand. Let d = annual demand for a product in units and p = price per unit. A... For most products, higher prices result in decreased demand, whereas lower prices result in increased demand. Let d = annual demand for a product in units and p = price per unit. Assume a firm accepts the following price-demand relationship as being realistic: d = 1,000 - 12p where p must be between $20 and $80. How many units can the firm sell at the $20 per-unit price? At the $80 per-unit price? What happens to annual units demanded for the product if the firm increases the per-unit price from $24 to $25? From $43 to $44? From $66 to $67? What is the suggested relationship between the per-unit price and annual demand for the product in units? Show the mathematical model for the total revenue (TR) in terms of p. Based on other considerations, the firm's management will only consider price alternatives of $28, $40, and $52. Use your model from part (b) to determine the price alternative that will maximize total revenue. What are the expected annual demand and the total revenue corresponding to your recommended price? Read more

Steps to Solve

1. Calculate units demanded at given prices To find the number of units sold at various price points, we can use the demand formula:
   $$ d = 1000 - 12p $$
   Substitute the price $p$ into the equation for each case.

2. Units sold at $20 per unit Substitute $p = 20$:
   $$ d = 1000 - 12(20) = 1000 - 240 = 760 $$
   The firm can sell 760 units at $20 per unit.

3. Units sold at $66 and $80 per unit For $p = 66$:
   $$ d = 1000 - 12(66) = 1000 - 792 = 208 $$
   For $p = 80$:
   $$ d = 1000 - 12(80) = 1000 - 960 = 40 $$
   The firm can sell 208 units at $66 and 40 units at $80.

4. Effect of price increase from $24 to $25 For $p = 24:
   $$ d = 1000 - 12(24) = 1000 - 288 = 712 $$
   For $p = 25:
   $$ d = 1000 - 12(25) = 1000 - 300 = 700 $$
   The demand decreases by 12 units as price increases, so the change is from 712 to 700.

5. Effect of price increase from $43 to $44 For $p = 43:
   $$ d = 1000 - 12(43) = 1000 - 516 = 484 $$
   For $p = 44:
   $$ d = 1000 - 12(44) = 1000 - 528 = 472 $$
   The demand decreases from 484 to 472 units.

6. Effect of price increase from $66 to $67 For $p = 66: Already calculated: $$ d = 208 $$
   For $p = 67:
   $$ d = 1000 - 12(67) = 1000 - 804 = 196 $$
   The demand decreases from 208 to 196 units.

7. Formulate the total revenue model (TR) Total revenue (TR) is given by:
   $$ TR = p \cdot d $$
   Substitute the demand equation:
   $$ TR = p(1000 - 12p) $$
   This simplifies to:
   $$ TR = 1000p - 12p^2 $$

8. Maximize total revenue Explore prices $28, $40, and $52 to find total revenue using the model derived.
   Calculate TR at each price based on the demand relationship.

   At $28:
   $$ d = 1000 - 12(28) = 1000 - 336 = 664 $$
   $$ TR = 28 \times 664 = 18592 $$

   At $40:
   $$ d = 1000 - 12(40) = 1000 - 480 = 520 $$
   $$ TR = 40 \times 520 = 20800 $$

   At $52:
   $$ d = 1000 - 12(52) = 1000 - 624 = 376 $$
   $$ TR = 52 \times 376 = 19552 $$

9. Determine maximum TR Compare TR values from prices $28, $40, and $52$. The maximum TR occurs at $40.