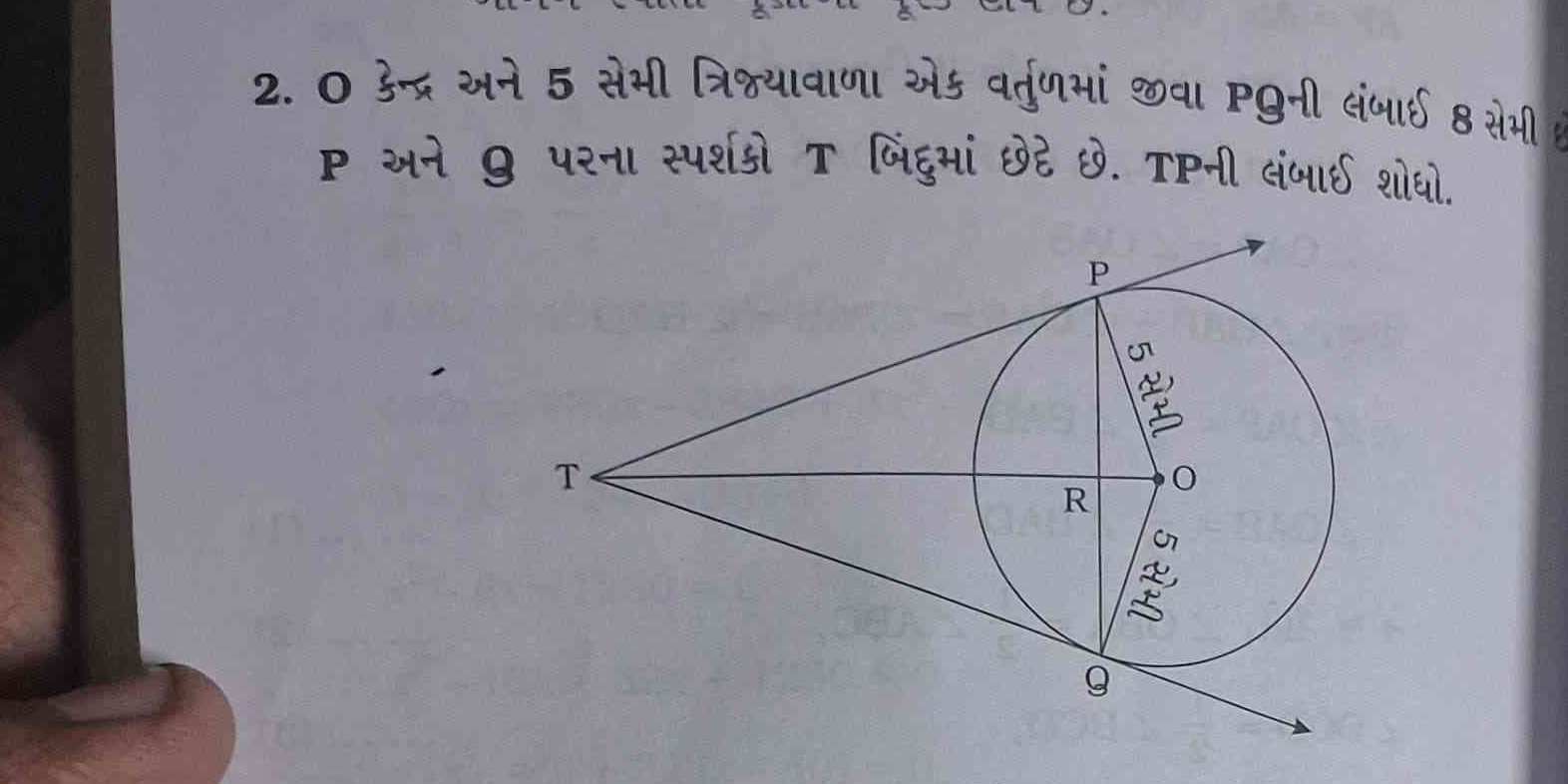
O કેન્દ્ર અને 5 સેમી ત્રિજ્યાવાળા એક વર્તુળમાં, જીવા PQ ની લંબાઈ 8 સેમી છે. P અને Q પરના સ્પર્શકો T બિંદુમાં છેદે છે. TP ની લંબાઈ શોધો. O કેન્દ્ર અને 5 સેમી ત્રિજ્યાવાળા એક વર્તુળમાં, જીવા PQ ની લંબાઈ 8 સેમી છે. P અને Q પરના સ્પર્શકો T બિંદુમાં છેદે છે. TP ની લંબાઈ શોધો. Read more

Steps to Solve

1. OR ની લંબાઈ શોધો

OR એ PQ નો અડધો ભાગ છે કારણ કે OR એ જીવા PQ ને લંબરૂપ છે. તેથી, $OR = \frac{1}{2} PQ = \frac{1}{2} \times 8 = 4$ સેમી.

2. $\triangle OPR$ માં પાયથાગોરસ પ્રમેયનો ઉપયોગ કરો

$\triangle OPR$ માં, $OP^2 = OR^2 + PR^2$. આપણને ખબર છે કે $OP = 5$ સેમી (ત્રિજ્યા) અને $OR = 4$ સેમી. તેથી,

$PR^2 = OP^2 - OR^2 = 5^2 - 4^2 = 25 - 16 = 9$ $PR = \sqrt{9} = 3$ સેમી

3. $\triangle OTP$ ને ધ્યાનમાં લો

$\triangle OTP$ કાટકોણ ત્રિકોણ છે, કારણ કે સ્પર્શક ત્રિજ્યાને લંબરૂપ હોય છે. તેથી, $\angle OPT = 90^\circ$. ધારો કે $TP = x$.

4. બે સમરૂપ ત્રિકોણો ઓળખો

$\triangle TRP \sim \triangle OTP$ કારણ કે બંને કાટકોણ ત્રિકોણ છે અને $\angle T = \angle T$ (સામાન્ય ખૂણો).

5. સમરૂપ ત્રિકોણોના ગુણધર્મોનો ઉપયોગ કરો

સમરૂપ ત્રિકોણોની બાજુઓ પ્રમાણસર હોય છે. તેથી, $\frac{TP}{OP} = \frac{RP}{TP}$

$\frac{x}{5} = \frac{3}{x}$ $x^2 = 5 \times 3 = 15$

હવે, આપણે $TR$ શોધવાની જરૂર છે અને પછી પાયથાગોરસ પ્રમેયનો ઉપયોગ કરીને $TP$ શોધી શકીએ છીએ.

$\triangle OTP$ માં, $OT^2 = OP^2 + TP^2$

અને $OT = OR + RT = 4 + RT$.

હવે બીજી રીતે સમરૂપતાનો ઉપયોગ કરીએ: $\triangle TPR \sim \triangle TPO$ $\frac{TP}{TO} = \frac{TR}{TP} = \frac{PR}{PO}$ $\frac{TP}{TO} = \frac{PR}{PO}$ $\frac{TP}{TO} = \frac{3}{5}$ $TO = \frac{5 \times TP}{3}$

$\frac{TR}{TP} = \frac{3}{5}$ $TR = \frac{3 \times TP}{5}$

$OR + TR = TO$ $4 + \frac{3 \times TP}{5} = \frac{5 \times TP}{3}$ ગુણાકાર કરતા, આપણને મળે છે $4 = TP (\frac{5}{3} - \frac{3}{5}) = TP (\frac{25 - 9}{15}) = TP \frac{16}{15}$ $TP = \frac{4 \times 15}{16} = \frac{15}{4}$

હવે, $TO^2 = TP^2 + PO^2$:

$(\frac{5}{3} TP)^2 = TP^2 + 5^2$ $(\frac{25}{9} - 1) TP^2 = 25$ $\frac{16}{9} TP^2 = 25$ $TP^2 = \frac{25 \times 9}{16}$ $TP = \frac{5 \times 3}{4} = \frac{15}{4} = 7.5$

આમ, $TP = \frac{20}{3}$.