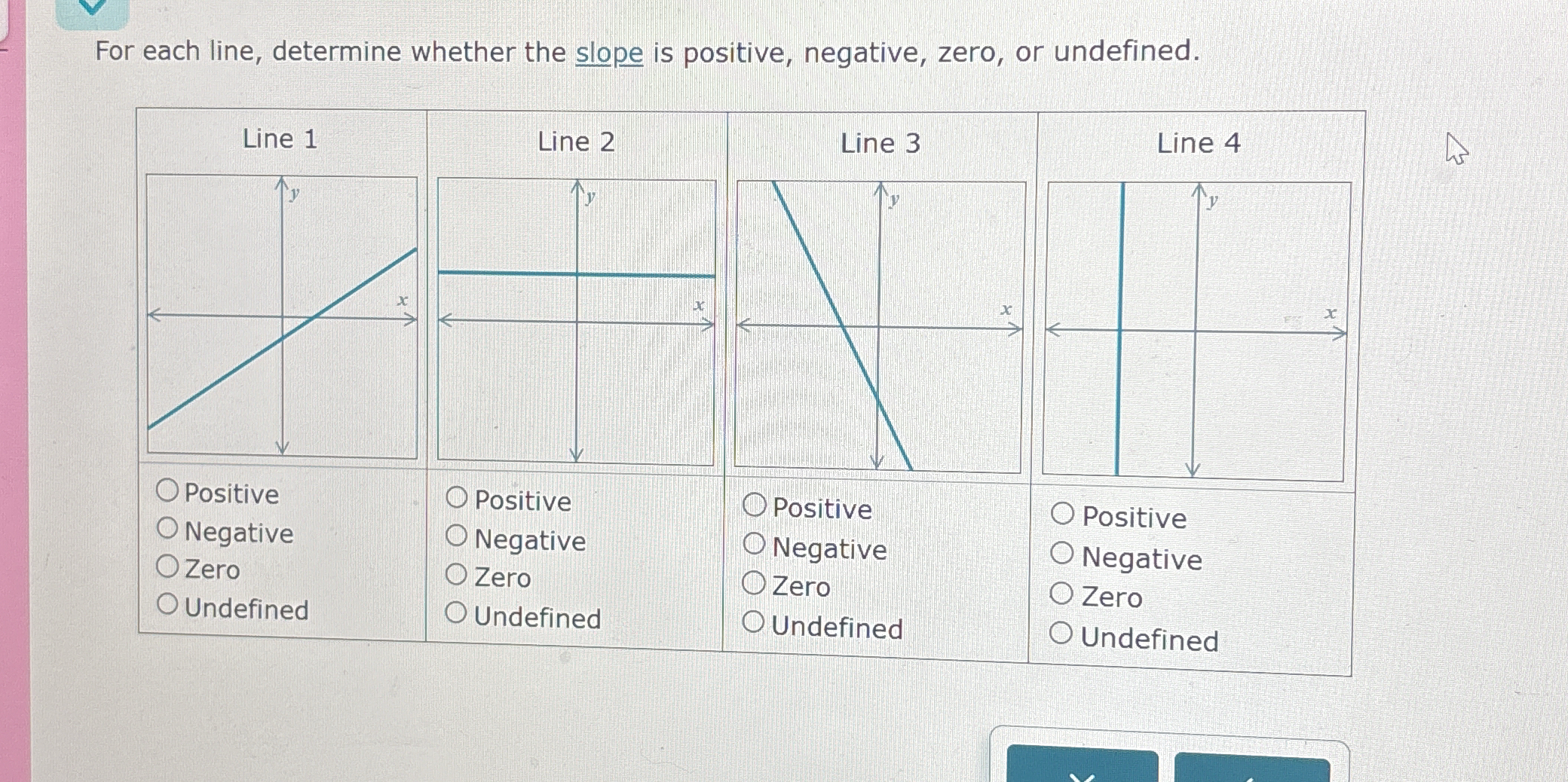
For each line, determine whether the slope is positive, negative, zero, or undefined.
Understand the Problem
The question asks to determine the slope of each line presented in the image. The options for the slope are positive, negative, zero, or undefined. We need to analyze the direction and orientation of each line to determine its slope.
Answer
Line 1: Positive Line 2: Zero Line 3: Negative Line 4: Undefined
Answer for screen readers
Line 1: Positive Line 2: Zero Line 3: Negative Line 4: Undefined
Steps to Solve
-
Analyze Line 1 Line 1 goes upwards from left to right. This indicates a positive slope.
-
Analyze Line 2 Line 2 is horizontal. Horizontal lines have a slope of zero because the $y$ value does not change.
-
Analyze Line 3 Line 3 goes downwards from left to right. This indicates a negative slope.
-
Analyze Line 4 Line 4 is vertical. Vertical lines have an undefined slope because the change in $x$ is zero, leading to division by zero in the slope formula. The slope is $\frac{\Delta y}{\Delta x}$, where $\Delta x = 0$.
Line 1: Positive Line 2: Zero Line 3: Negative Line 4: Undefined
More Information
The slope of a line describes its steepness and direction. A positive slope means the line goes up from left to right, a negative slope means it goes down from left to right, a zero slope means it is horizontal, and an undefined slope means it is vertical.
Tips
A common mistake is confusing a zero slope with an undefined slope. Horizontal lines (zero slope) are often confused with vertical lines (undefined slope). Remembering that slope is rise over run ($\frac{\Delta y}{\Delta x}$) helps: horizontal lines have no rise ($\Delta y = 0$), while vertical lines have no run ($\Delta x = 0$), leading to division by zero, hence undefined.
AI-generated content may contain errors. Please verify critical information