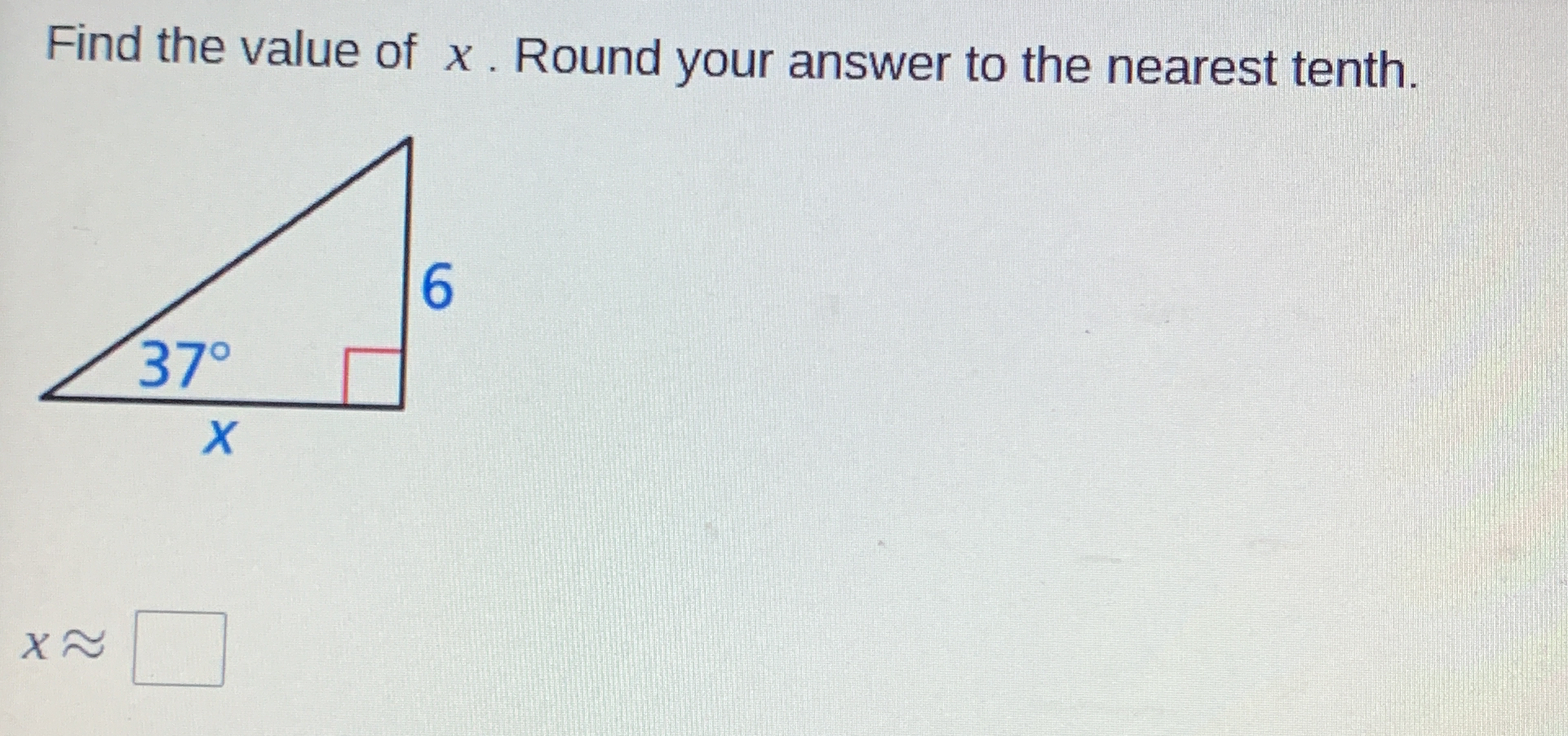
Find the value of x. Round your answer to the nearest tenth.

Steps to Solve

1. Identify the appropriate trigonometric function

Since we have a right triangle and we know the angle (37 degrees) and the side opposite this angle (6), we will use the sine function, which is defined as: $$ \sin(\theta) = \frac{\text{opposite}}{\text{hypotenuse}} $$

2. Set up the equation using sine

We need to express the sine of the angle in terms of the known values. Let's substitute our values into the equation: $$ \sin(37^\circ) = \frac{6}{\text{hypotenuse}} $$

3. Calculate the hypotenuse

To find the hypotenuse, we can rearrange the equation: $$ \text{hypotenuse} = \frac{6}{\sin(37^\circ)} $$

4. Find the value of $\sin(37^\circ)$

Using a calculator, we find: $$ \sin(37^\circ) \approx 0.6018 $$

5. Substitute the sine value into the equation

Now, plug in the sine value: $$ \text{hypotenuse} \approx \frac{6}{0.6018} $$

6. Calculate the hypotenuse

Perform the calculation: $$ \text{hypotenuse} \approx 9.966 $$

7. Use the Pythagorean theorem to find x

Now we can find the adjacent side, (x), using the Pythagorean theorem: $$ x^2 + 6^2 = (9.966)^2 $$

8. Calculate (x^2)

First, calculate ((9.966)^2): $$ (9.966)^2 \approx 99.33 $$ Then calculate (6^2 = 36).

Substitute into the Pythagorean theorem: $$ x^2 + 36 = 99.33 $$

9. Solve for (x^2)

Rearranging gives: $$ x^2 = 99.33 - 36 $$

10. Calculate (x)

Now perform the subtraction: $$ x^2 = 63.33 $$

Finally, take the square root: $$ x \approx \sqrt{63.33} \approx 7.96 $$

Rounding to the nearest tenth: $$ x \approx 8.0 $$