Find the value of k which makes the equation $kx^2 + 5x - \frac{5}{4} = 0$ to have equal roots.
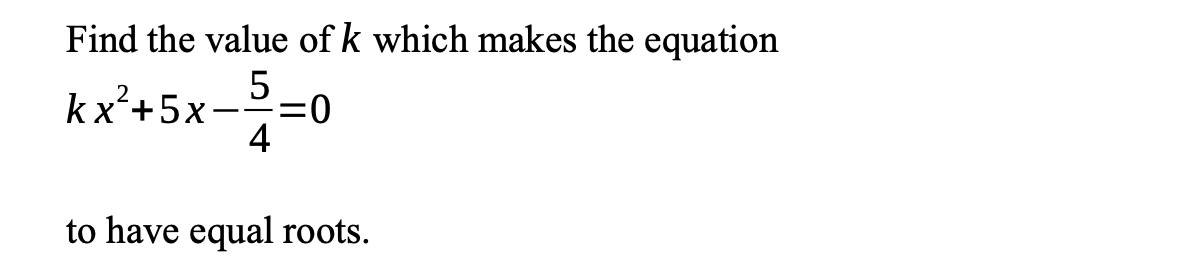
Understand the Problem
The question asks to find the value of 'k' such that the given quadratic equation has equal roots. This involves using the discriminant (b^2 - 4ac) of the quadratic formula. For equal roots, the discriminant must be equal to zero. We'll set up and solve this equation to find 'k'.
Answer
$k = -5$
Answer for screen readers
$k = -5$
Steps to Solve
-
Identify coefficients We have the quadratic equation $kx^2 + 5x - \frac{5}{4} = 0$. We need to identify the coefficients $a$, $b$, and $c$. Here, $a = k$, $b = 5$, and $c = -\frac{5}{4}$.
-
Apply the discriminant condition For equal roots, the discriminant ($b^2 - 4ac$) must be zero. So, we have $b^2 - 4ac = 0$.
-
Substitute coefficients into the discriminant Substitute the values of $a$, $b$, and $c$ into the discriminant equation: $5^2 - 4 \cdot k \cdot (-\frac{5}{4}) = 0$
-
Simplify the equation Simplify the equation: $25 + 5k = 0$
-
Solve for k Solve the linear equation for $k$: $5k = -25$ $k = \frac{-25}{5}$ $k = -5$
$k = -5$
More Information
The value of $k$ that makes the quadratic equation have equal roots is $-5$. This means when $k = -5$, the equation becomes $-5x^2 + 5x - \frac{5}{4} = 0$, which has a repeated root.
Tips
A common mistake is to incorrectly identify the coefficients $a$, $b$, and $c$. Ensure you correctly map each term to its corresponding coefficient. Also, watch out for the signs when substituting into the discriminant formula, especially when $c$ is negative.
AI-generated content may contain errors. Please verify critical information