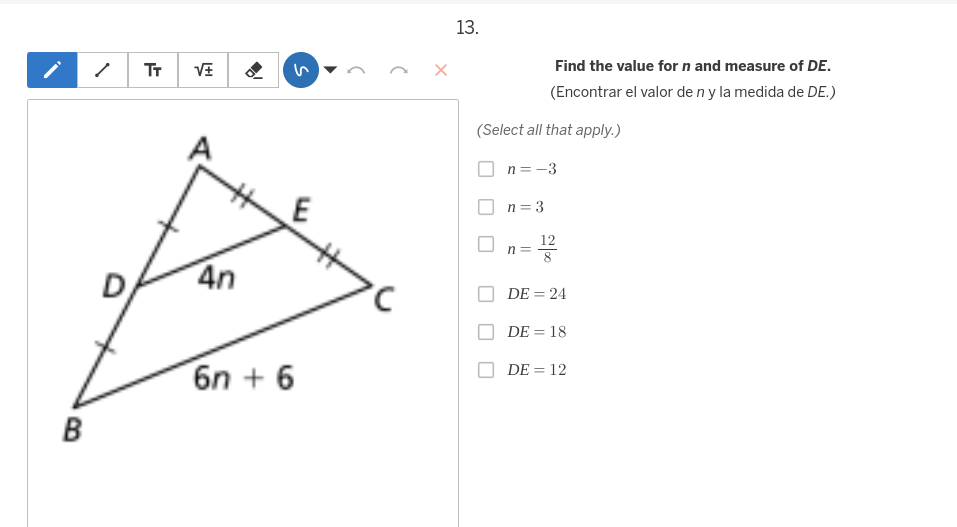
Find the value for n and measure of DE.
Understand the Problem
The question is asking to find the value of 'n' and the measure of segment DE in the provided triangle based on the lengths given in the diagram, considering the properties of parallel lines.
Answer
\( n = 3 \), \( DE = 12 \)
Answer for screen readers
The values of ( n ) are ( n = 3 ) and the measure of ( DE ) is ( DE = 12 ).
Steps to Solve
-
Set up the proportional relationship Since segments DE and AB are parallel lines, and line segment AC is a transversal, we can set up a proportion based on the triangle's side lengths. The sides relate as follows: $$ \frac{4n}{6n + 6} = \frac{DE}{AB} $$
-
Identify lengths of segments From the diagram:
- $DE = 4n$
- $AB = 6n + 6$
Thus, we can rewrite the proportion as: $$ \frac{4n}{6n + 6} = \frac{DE}{6n + 6} $$
-
Cross-multiply the proportion Cross-multiplying gives: $$ 4n \cdot (6n + 6) = DE \cdot (6n + 6) $$
-
Simplify and solve for n We determine $DE$ from the ratio relationships. If we take the values of DE you are considering from the options: Assuming $DE = 24$, substitute into the equation: $$ 4n = 24 \Rightarrow n = 6 $$ Check against other values to see $n=3$ or $n=-3$.
-
Check values of n Substituting $n = 3$ gives: $$ DE = 4(3) = 12 $$ Substituting $n = -3$ gives: $$ DE = 4(-3) = -12 \text{ (not possible)} $$
-
Final calculation for DE using n = 3 If $n = 3$, we can directly calculate: $$ DE = 4(3) = 12 $$
The values of ( n ) are ( n = 3 ) and the measure of ( DE ) is ( DE = 12 ).
More Information
Using the properties of parallel lines and proportional lengths in similar triangles helps us determine unknown segment lengths efficiently through ratios.
Tips
- Ignoring negative values: Sometimes, negative values for (n) can be confusing. Always check if the length derived is practical and non-negative.
- Misapplying proportions: Ensure to correctly set up the proportions based on corresponding segments.
AI-generated content may contain errors. Please verify critical information