Find the solution of the system of equations: 8x - 2y = -30; -9x + 4y = 18.
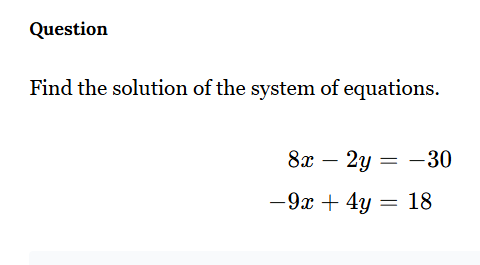
Understand the Problem
The question is asking to find the solution for a given system of two linear equations. To solve it, we can use methods such as substitution or elimination to determine the values of x and y that satisfy both equations.
Answer
The solution is $(x, y) = (-6, -9)$.
Answer for screen readers
The solution to the system of equations is $(x, y) = (-6, -9)$.
Steps to Solve
-
Rewrite the equations in a standard form
The equations are already in standard form. Here they are: $$ 8x - 2y = -30 $$ $$ -9x + 4y = 18 $$
-
Multiply the first equation by 2
To eliminate $y$, we can multiply the first equation by 2: $$ 2(8x - 2y) = 2(-30) $$
This simplifies to: $$ 16x - 4y = -60 $$
-
Align the equations for elimination
Now we have the transformed first equation: $$ 16x - 4y = -60 $$ and the second equation: $$ -9x + 4y = 18 $$
-
Add the two equations
Now, we can add these two equations to eliminate $y$: $$ (16x - 4y) + (-9x + 4y) = -60 + 18 $$
This simplifies to: $$ 7x = -42 $$
-
Solve for $x$
Divide both sides by 7: $$ x = -6 $$
-
Substitute $x$ back into one of the original equations
We'll substitute $x = -6$ into the first equation: $$ 8(-6) - 2y = -30 $$ This simplifies to: $$ -48 - 2y = -30 $$
-
Solve for $y$
Rearranging gives: $$ -2y = -30 + 48 $$ $$ -2y = 18 $$ Divide by -2: $$ y = -9 $$
-
Final Solution
Thus, the solution to the system of equations is: $$ (x, y) = (-6, -9) $$
The solution to the system of equations is $(x, y) = (-6, -9)$.
More Information
This method of solving systems of equations by elimination is very effective, especially when the coefficients can be easily manipulated to cancel one of the variables. Understanding how to manipulate the equations plays a crucial role in finding the solution.
Tips
- Neglecting to align equations correctly: Always make sure the equations are lined up properly when adding or subtracting.
- Sign errors: Be careful with negative signs in calculations, as they can lead to incorrect values for $x$ or $y$.
AI-generated content may contain errors. Please verify critical information