Find the quotient: (9m^7 - 27m^3 + 81m^2) / (18m^3)
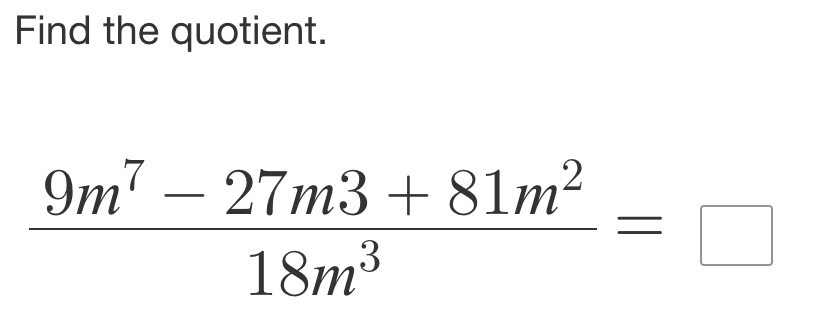
Understand the Problem
The question asks us to find the quotient of the given expression. This involves dividing each term in the numerator by the denominator and simplifying the resulting expression.
Answer
$\frac{1}{2}m^4 - \frac{3}{2} + \frac{9}{2m}$
Answer for screen readers
$\frac{1}{2}m^4 - \frac{3}{2} + \frac{9}{2m}$
Steps to Solve
- Divide each term in the numerator by the denominator
We will split the fraction into three separate fractions:
$$ \frac{9m^7 - 27m^3 + 81m^2}{18m^3} = \frac{9m^7}{18m^3} - \frac{27m^3}{18m^3} + \frac{81m^2}{18m^3} $$
- Simplify each fraction
Simplify each fraction by dividing the coefficients and subtracting the exponents of $m$
$$ \frac{9m^7}{18m^3} = \frac{1}{2}m^{7-3} = \frac{1}{2}m^4 $$ $$ \frac{27m^3}{18m^3} = \frac{3}{2}m^{3-3} = \frac{3}{2}m^0 = \frac{3}{2} $$ $$ \frac{81m^2}{18m^3} = \frac{9}{2}m^{2-3} = \frac{9}{2}m^{-1} = \frac{9}{2m} $$
- Combine the simplified fractions
Now we combine the simplified fractions:
$$ \frac{1}{2}m^4 - \frac{3}{2} + \frac{9}{2m} $$
$\frac{1}{2}m^4 - \frac{3}{2} + \frac{9}{2m}$
More Information
The quotient represents the result of dividing one expression by another. In this case, we divided a polynomial by a monomial.
Tips
A common mistake is to not simplify the fractions completely. For example, leaving $\frac{9}{18}$ as is instead of simplifying to $\frac{1}{2}$. Another common mistake is with the exponent rules, specifically when dividing like variables. Remember to subtract the exponents.
AI-generated content may contain errors. Please verify critical information