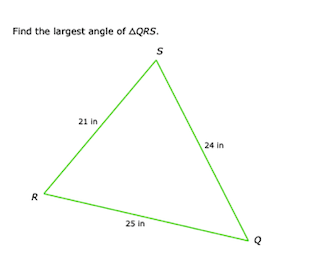
Find the largest angle of triangle SQR.

Steps to Solve

1. Identify the sides and the angle to find

The triangle sides are given as follows:

• ( a = 21 ) in (opposite to angle ( Q ))
• ( b = 24 ) in (opposite to angle ( R ))
• ( c = 25 ) in (opposite to angle ( S ))

We want to find the largest angle, which is opposite the longest side, angle ( S ).

2. Apply the Law of Cosines

To find angle ( S ), use the Law of Cosines, which states:

$$ c^2 = a^2 + b^2 - 2ab \cdot \cos(S) $$

Substituting the values we have:

$$ 25^2 = 21^2 + 24^2 - 2(21)(24) \cdot \cos(S) $$

3. Calculate each term

Calculating ( a^2 ), ( b^2 ), and ( c^2 ):

• ( 25^2 = 625 )
• ( 21^2 = 441 )
• ( 24^2 = 576 )

Substituting these values into the equation gives:

$$ 625 = 441 + 576 - 2(21)(24) \cdot \cos(S) $$

Calculating ( 441 + 576 ):

$$ 625 = 1017 - 2(21)(24) \cdot \cos(S) $$

4. Isolate (\cos(S))

Rearranging gives:

$$ 2(21)(24) \cdot \cos(S) = 1017 - 625 $$

Calculating ( 1017 - 625 ):

$$ 2(21)(24) \cdot \cos(S) = 392 $$

Now, divide both sides by ( 2(21)(24) ):

$$ \cos(S) = \frac{392}{2(21)(24)} $$

Calculating the denominator:

$$ 2(21)(24) = 1008 $$

So,

$$ \cos(S) = \frac{392}{1008} $$

5. Calculate (\cos(S)) and then find angle ( S )

This simplifies to:

$$ \cos(S) = \frac{49}{126} = \frac{7}{18} $$

Now, use the inverse cosine to find angle ( S ):

$$ S = \cos^{-1}\left(\frac{7}{18}\right) $$

Calculating this:

$$ S \approx 61.35^\circ $$ (rounded to two decimal places)