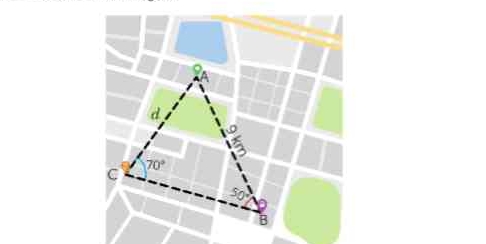
Find the distance 'd' from point A to point C in the triangle, given the map with distance from A to B = 9 km, angle at C = 70 degrees, and angle at B = 50 degrees.

Steps to Solve

1. Calculate the angle at vertex A Since the sum of angles in a triangle is 180 degrees, we can find the angle at vertex A using the formula: $A = 180^\circ - B - C$ $A = 180^\circ - 50^\circ - 70^\circ = 60^\circ$

2. Apply the Law of Sines The Law of Sines states that the ratio of the length of a side to the sine of its opposite angle is constant for all sides and angles in a triangle. We can set up the following proportion to find the length of side AC (which we're calling d): $\frac{AB}{\sin C} = \frac{AC}{\sin B}$ $\frac{9}{\sin 70^\circ} = \frac{d}{\sin 50^\circ}$

3. Solve for d Multiply both sides of the equation by $\sin 50^\circ$ to isolate d: $d = \frac{9 \cdot \sin 50^\circ}{\sin 70^\circ}$

4. Calculate the value of d Using a calculator: $\sin 50^\circ \approx 0.766$ $\sin 70^\circ \approx 0.940$ $d \approx \frac{9 \cdot 0.766}{0.940} \approx \frac{6.894}{0.940} \approx 7.334$