Find the characteristic equation of A = [[3, 10, 5], [-2, -3, -4], [3, 5, 7]]
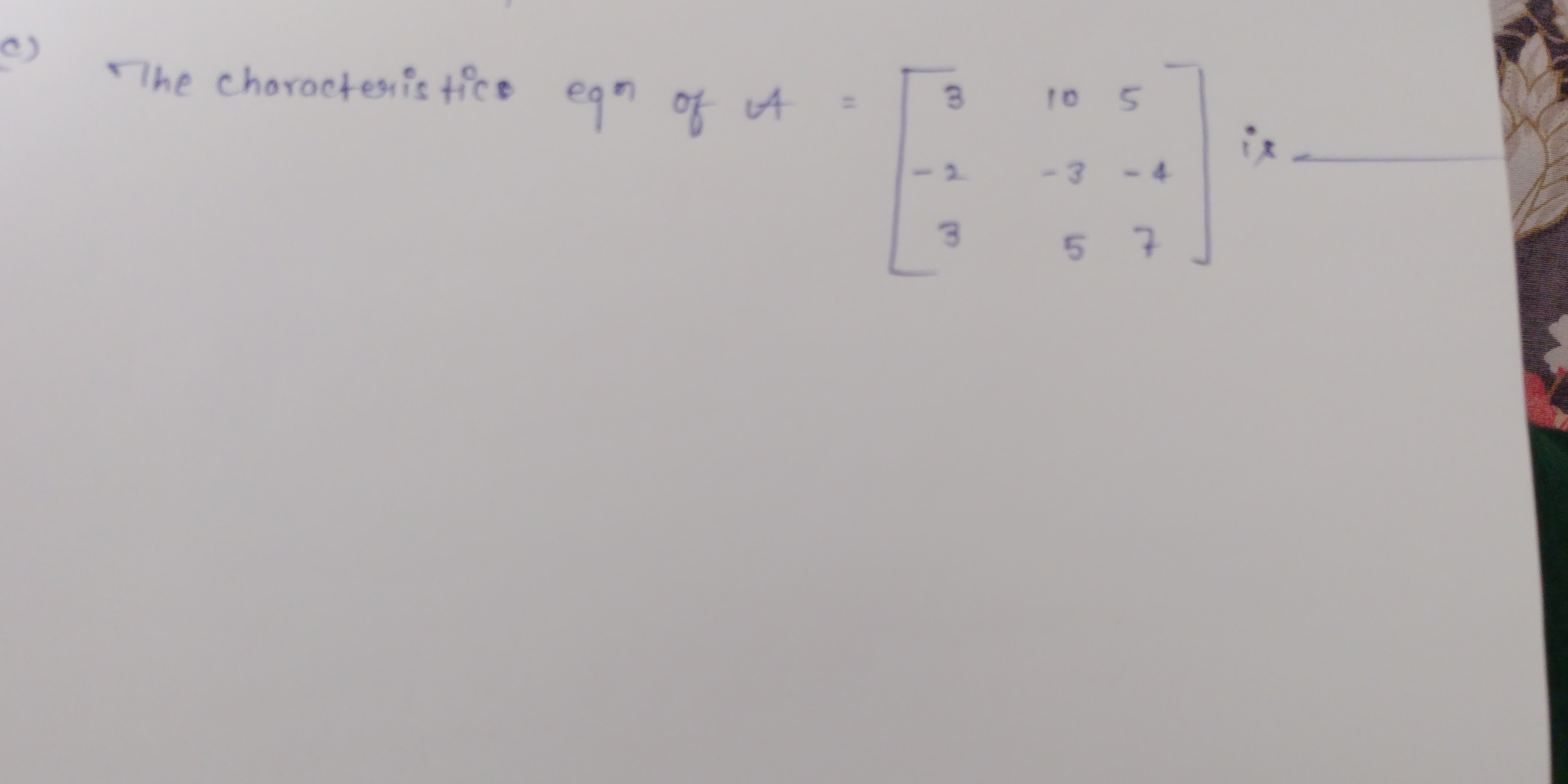
Understand the Problem
The question is asking for the characteristic equation of a matrix A provided in the image. The characteristic equation is typically derived from the determinant of the matrix subtracted by a scalar (usually denoted as λ) times the identity matrix, set equal to zero.
Answer
The characteristic equation is $ (3 - \lambda)((-3 - \lambda)(7 - \lambda) + 20) - 10(2\lambda - 2) + 5(3\lambda - 1) = 0 $.
Answer for screen readers
The characteristic equation of the matrix $A$ is given by:
$$ (3 - \lambda)\left((-3 - \lambda)(7 - \lambda) + 20\right) - 10(2\lambda - 2) + 5(3\lambda - 1) = 0. $$
Steps to Solve
- Set Up the Characteristic Equation
To find the characteristic equation, we start by forming the matrix $A - \lambda I$, where $I$ is the identity matrix and $\lambda$ is the scalar.
Given the matrix
$$ A = \begin{bmatrix} 3 & 10 & 5 \ -2 & -3 & -4 \ 3 & 5 & 7 \end{bmatrix}, $$
the identity matrix $I$ of size 3 is
$$ I = \begin{bmatrix} 1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \end{bmatrix}. $$
Thus, the equation becomes
$$ A - \lambda I = \begin{bmatrix} 3 - \lambda & 10 & 5 \ -2 & -3 - \lambda & -4 \ 3 & 5 & 7 - \lambda \end{bmatrix}. $$
- Calculate the Determinant
Next, we need to find the determinant of the matrix $A - \lambda I$.
We can compute this as follows:
$$ \text{det}(A - \lambda I) = \begin{vmatrix} 3 - \lambda & 10 & 5 \ -2 & -3 - \lambda & -4 \ 3 & 5 & 7 - \lambda \end{vmatrix}. $$
Using cofactor expansion along the first row, this gives us:
$$ \text{det}(A - \lambda I) = (3 - \lambda) \begin{vmatrix} -3 - \lambda & -4 \ 5 & 7 - \lambda \end{vmatrix} - 10 \begin{vmatrix} -2 & -4 \ 3 & 7 - \lambda \end{vmatrix} + 5 \begin{vmatrix} -2 & -3 - \lambda \ 3 & 5 \end{vmatrix}. $$
- Evaluate the 2x2 Determinants
We now find the three 2x2 determinants.
- For the first determinant:
$$ \begin{vmatrix} -3 - \lambda & -4 \ 5 & 7 - \lambda \end{vmatrix} = (-3 - \lambda)(7 - \lambda) - (-4)(5) = (-3 - \lambda)(7 - \lambda) + 20. $$
- For the second determinant:
$$ \begin{vmatrix} -2 & -4 \ 3 & 7 - \lambda \end{vmatrix} = (-2)(7 - \lambda) - (-4)(3) = -14 + 2\lambda + 12 = 2\lambda - 2. $$
- For the third determinant:
$$ \begin{vmatrix} -2 & -3 - \lambda \ 3 & 5 \end{vmatrix} = (-2)(5) - (-3 - \lambda)(3) = -10 + 9 + 3\lambda = 3\lambda - 1. $$
- Combine Results and Set to Zero
Now substituting these determinations back:
$$ \text{det}(A - \lambda I) = (3 - \lambda)((-3 - \lambda)(7 - \lambda) + 20) - 10(2\lambda - 2) + 5(3\lambda - 1). $$
- Simplify to Form Characteristic Equation
Expand and simplify the resulting equation to find the characteristic polynomial, then set it equal to zero.
The characteristic equation of the matrix $A$ is given by:
$$ (3 - \lambda)\left((-3 - \lambda)(7 - \lambda) + 20\right) - 10(2\lambda - 2) + 5(3\lambda - 1) = 0. $$
More Information
The characteristic equation is fundamental in determining the eigenvalues of the matrix. The eigenvalues are crucial for understanding the behavior of linear transformations, stability in systems, and dimensional analysis in various fields including physics and engineering.
Tips
- Not properly subtracting $\lambda I$ from $A$.
- Errors in calculating determinants or not using the necessary row or column for cofactor expansion.
- Forgetting to set the determinant to zero to find the characteristic equation.
AI-generated content may contain errors. Please verify critical information