सिद्ध कीजिए कि फलन f(x) = |x-1|, x = 1 पर संतत है।
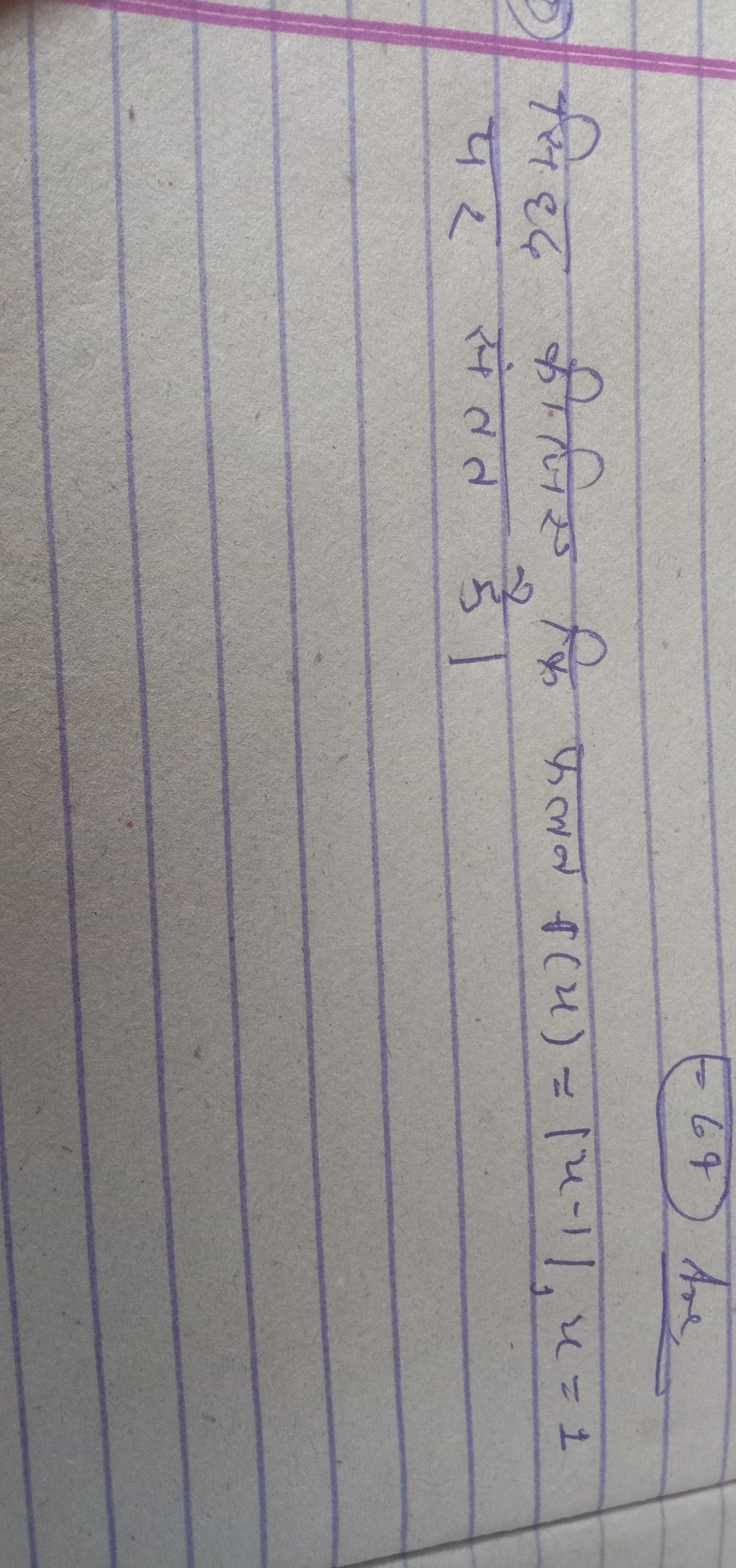
Understand the Problem
यह प्रश्न सिद्ध करने के लिए कह रहा है कि फलन f(x) = |x-1|, x = 1 पर संतत है। संतत का मतलब है कि फलन का ग्राफ उस बिंदु पर बिना टूटे या कूद के खींचा जा सकता है।
Answer
चूंकि $\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1) = 0$, फलन $f(x) = |x - 1|$, $x = 1$ पर संतत है।
Answer for screen readers
फलन $f(x) = |x - 1|$, $x = 1$ पर संतत है क्योंकि $\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1) = 0$.
Steps to Solve
-
फलन को परिभाषित करना दिए गए फलन को इस प्रकार परिभाषित किया गया है: $$ f(x) = |x - 1| $$
-
निरंतरता के लिए शर्त $x = 1$ पर फलन को संतत सिद्ध करने के लिए, हमें यह दिखाना होगा कि: $$ \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1) $$ यहाँ, $\lim_{x \to 1^-} f(x)$ बायीं सीमा है, $\lim_{x \to 1^+} f(x)$ दायीं सीमा है, और $f(1)$ $x = 1$ पर फलन का मान है।
-
बायीं सीमा ज्ञात करना बायीं सीमा के लिए, हम $x$, $1$ की ओर नीचे से बढ़ता है: $$ \lim_{x \to 1^-} f(x) = \lim_{x \to 1^-} |x - 1| $$ जब $x$, $1$ से थोड़ा कम है, तो $x - 1$ ऋणात्मक है, इसलिए $|x - 1| = -(x - 1) = 1 - x$: $$ \lim_{x \to 1^-} (1 - x) = 1 - 1 = 0 $$
-
दायीं सीमा ज्ञात करना दायीं सीमा के लिए, हम $x$, $1$ की ओर ऊपर से बढ़ता है: $$ \lim_{x \to 1^+} f(x) = \lim_{x \to 1^+} |x - 1| $$ जब $x$, $1$ से थोड़ा अधिक है, तो $x - 1$ धनात्मक है, इसलिए $|x - 1| = x - 1$: $$ \lim_{x \to 1^+} (x - 1) = 1 - 1 = 0 $$
-
फलन का मान ज्ञात करना $x = 1$ पर फलन का मान ज्ञात करना: $$ f(1) = |1 - 1| = |0| = 0 $$
-
निष्कर्ष चूंकि बायीं सीमा, दायीं सीमा और फलन का मान सभी बराबर हैं: $$ \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1) = 0 $$ इसलिए, फलन $f(x) = |x - 1|$, $x = 1$ पर संतत है।
फलन $f(x) = |x - 1|$, $x = 1$ पर संतत है क्योंकि $\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1) = 0$.
More Information
निरंतरता की अवधारणा कैलकुलस और गणितीय विश्लेषण में एक आधारशिला है। यह हमें फलन के व्यवहार को समझने और अनुमान लगाने में मदद करता है।
Tips
शून्य।
AI-generated content may contain errors. Please verify critical information