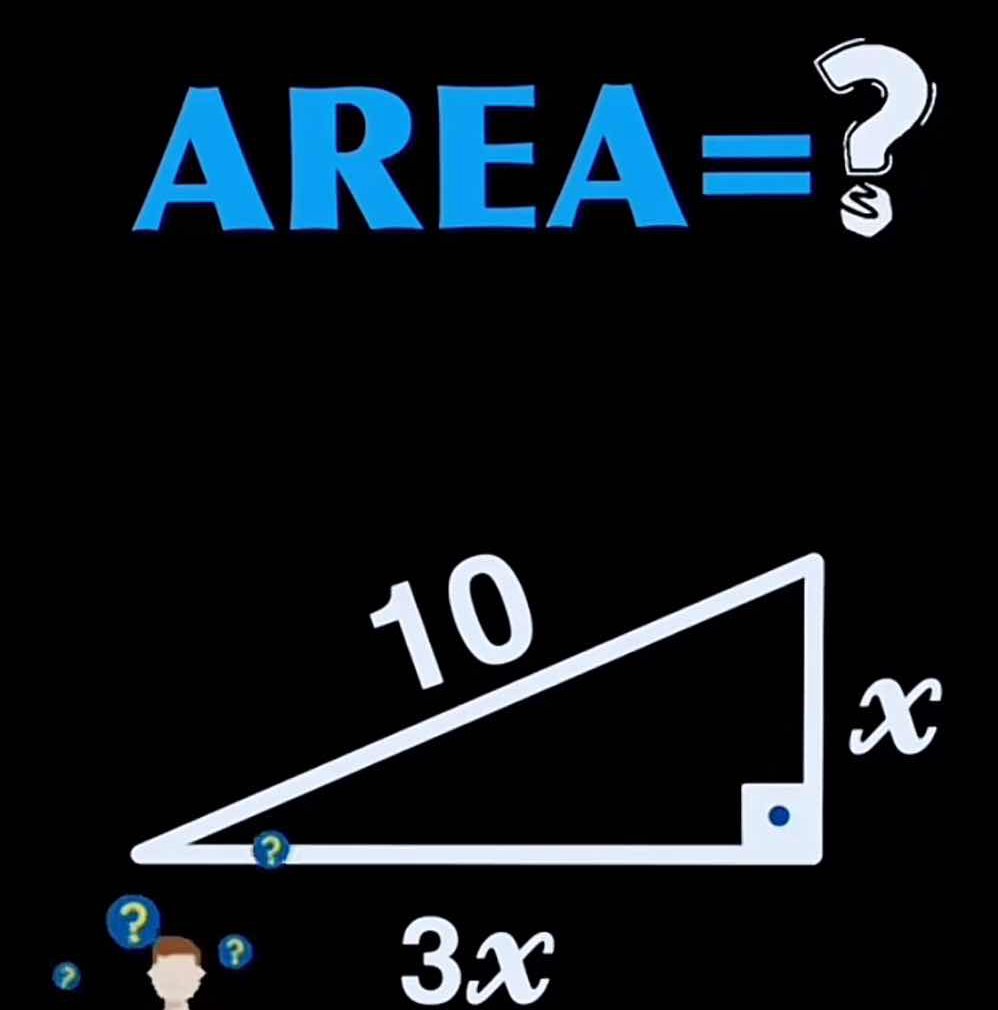
Find the area of the right angle triangle, given hypotenuse=10, height=x, base=3x.

Steps to Solve

1. Apply the Pythagorean theorem

Since we have a right-angled triangle, we can use the Pythagorean theorem: $a^2 + b^2 = c^2$, where $a$ and $b$ are the lengths of the two shorter sides (legs), and $c$ is the length of the hypotenuse. In our case, $a = x$, $b = 3x$, and $c = 10$.

2. Substitute the given values into the Pythagorean theorem equation

Substituting the values, we get: $x^2 + (3x)^2 = 10^2$

3. Simplify and solve for x

Simplifying the equation gives: $x^2 + 9x^2 = 100$ $10x^2 = 100$ $x^2 = 10$ $x = \sqrt{10}$

4. Calculate the lengths of the legs

We found that $x = \sqrt{10}$. Therefore, the lengths of the legs are: Leg 1: $x = \sqrt{10}$ Leg 2: $3x = 3\sqrt{10}$

5. Calculate the area of the triangle

The area of a right-angled triangle is given by: Area $= \frac{1}{2} \times \text{base} \times \text{height}$. In this case: Area $= \frac{1}{2} \times x \times 3x = \frac{1}{2} \times \sqrt{10} \times 3\sqrt{10}$

6. Simplify the area

Area $= \frac{1}{2} \times 3 \times 10 = \frac{30}{2} = 15$