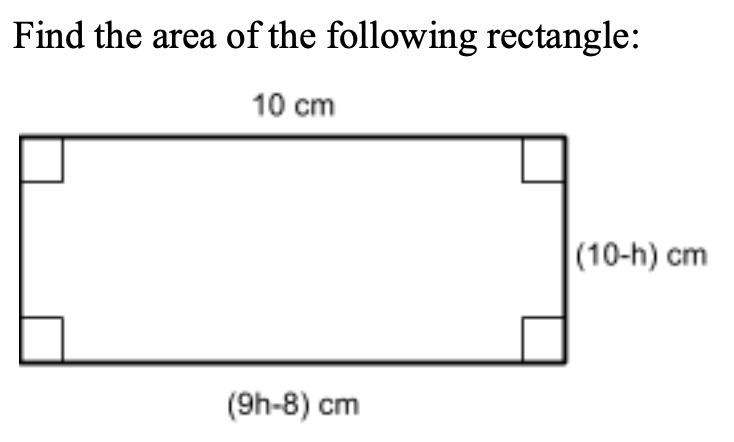
Find the area of the following rectangle: (9h-8) cm and (10-h) cm.
Understand the Problem
The question asks to find the area of a rectangle given its dimensions in terms of variables. We will calculate the area using the formula for the area of a rectangle, which is length multiplied by width.
Answer
The area of the rectangle is \( A = 90h - 80 \text{ cm}^2 \).
Answer for screen readers
The area of the rectangle is given by the expression ( A = 90h - 80 \text{ cm}^2 ).
Steps to Solve
- Identify Dimensions of the Rectangle
The length of the rectangle is given as $10 \text{ cm}$, and the width is represented by the expression $(9h - 8) \text{ cm}$.
- Write the Area Formula
The area ( A ) of a rectangle is calculated using the formula:
$$ A = \text{length} \times \text{width} $$
- Substitute the Dimensions into the Formula
Now we substitute the dimensions into the formula for area:
$$ A = 10 \text{ cm} \times (9h - 8) \text{ cm} $$
- Distribute the Length
Next, distribute the length over the width:
$$ A = 10(9h - 8) $$
- Simplify the Expression
Now, simplifying the expression gives:
$$ A = 90h - 80 $$
The area of the rectangle is given by the expression ( A = 90h - 80 \text{ cm}^2 ).
More Information
The area calculated is a function of the variable ( h ), indicating how the area changes based on different values of ( h ). Understanding how area is calculated using variables is crucial in algebra.
Tips
- Misunderstanding the dimensions: Ensure that the correct expressions for length and width are used directly from the diagram.
- Incorrect distribution: When multiplying, be careful to distribute correctly to avoid errors.
AI-generated content may contain errors. Please verify critical information