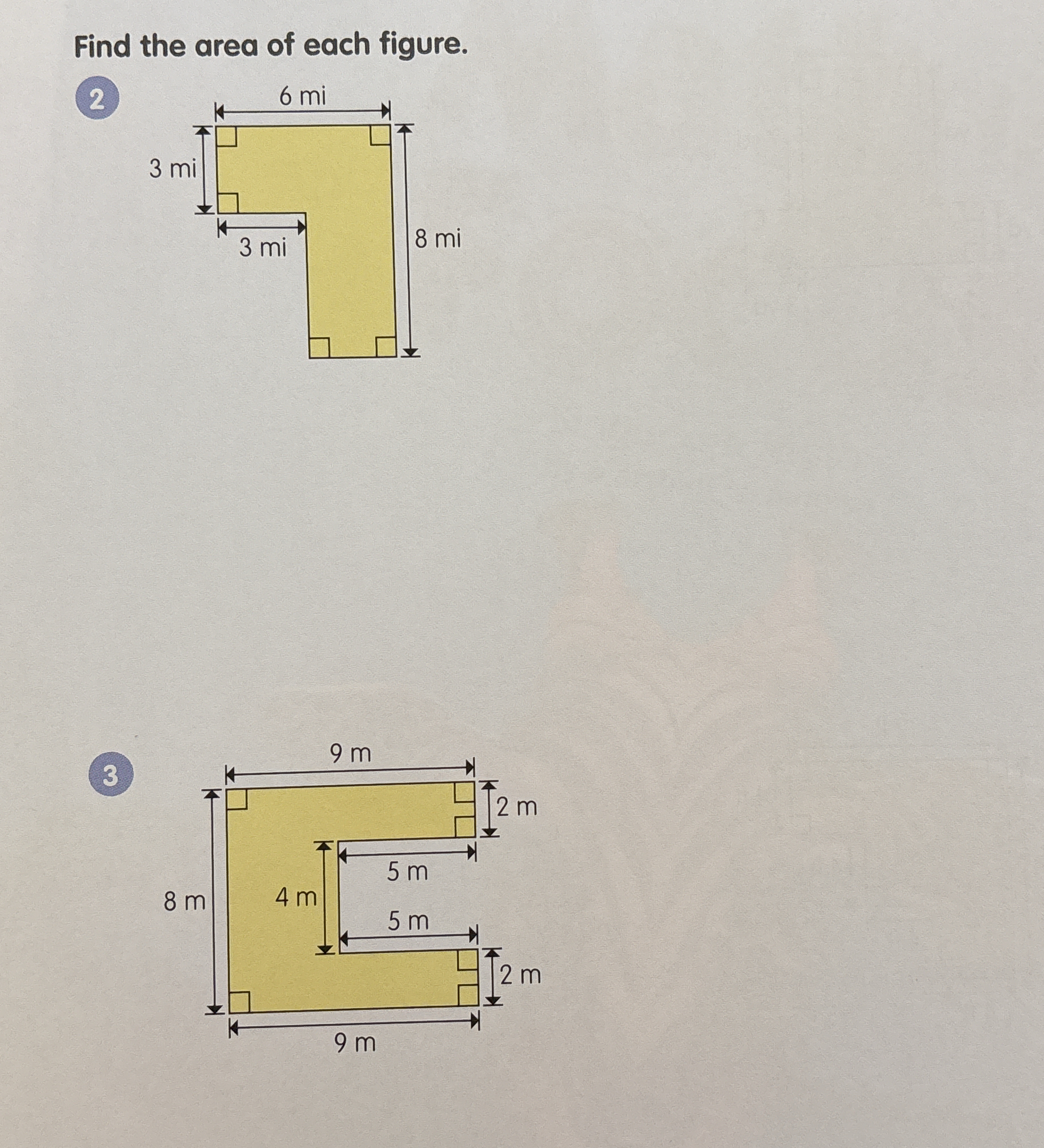
Find the area of each figure.
Understand the Problem
The question asks to find the area of two composite figures. We can find the area of each figure by dividing each of them into rectangles and summing them together. Figure 2 can be divided into two rectangles and figure 3 can be regarded as a big rectangle minus a smaller rectangle.
Answer
The area of the first figure is $42 \text{ mi}^2$. The area of the second figure is $52 \text{ m}^2$.
Answer for screen readers
The area of the first figure is $42 \text{ mi}^2$. The area of the second figure is $52 \text{ m}^2$.
Steps to Solve
- Divide the first figure into two rectangles
We can divide the first figure into a $6 \text{ mi} \times 3 \text{ mi}$ rectangle and a $3 \text{ mi} \times 8 \text{ mi}$ rectangle.
- Calculate the area of each rectangle
The area of the first rectangle is: $A_1 = 6 \text{ mi} \times 3 \text{ mi} = 18 \text{ mi}^2$ The area of the second rectangle is: $A_2 = 3 \text{ mi} \times 8 \text{ mi} = 24 \text{ mi}^2$
- Sum them to find the total area
The total area of the first figure is: $A = A_1 + A_2 = 18 \text{ mi}^2 + 24 \text{ mi}^2 = 42 \text{ mi}^2$
- Calculate the area of the big rectangle for the second figure
The big rectangle is $9 \text{ m} \times 8 \text{ m}$. Its area is: $A_1 = 9 \text{ m} \times 8 \text{ m} = 72 \text{ m}^2$
- Calculate the area of the small rectangle for the second figure
The small rectangle is $5 \text{ m} \times 4 \text{ m}$. Its area is: $A_2 = 5 \text{ m} \times 4 \text{ m} = 20 \text{ m}^2$
- Subtract them to find the total area of the second figure
The total area of the second figure can be calculated as the area of the big rectangle - the area of the small rectangle. $A = A_1 - A_2 = 72 \text{ m}^2 - 20 \text{ m}^2 = 52 \text{ m}^2$
The area of the first figure is $42 \text{ mi}^2$. The area of the second figure is $52 \text{ m}^2$.
More Information
The composite figures are made by combining different rectangles. The total area can still be calculated by dividing figures into rectangles we know how calculate area, and sum or subtract them to calculate the total area.
Tips
Null
AI-generated content may contain errors. Please verify critical information