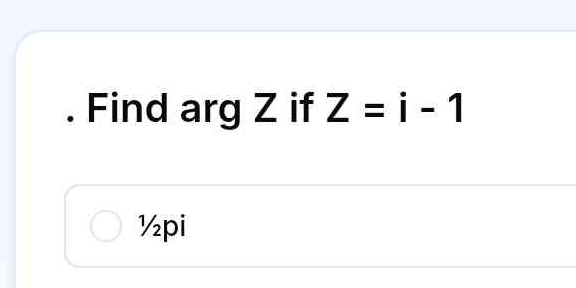
Find arg Z if Z = i - 1
Understand the Problem
The question is asking to find the argument of a complex number Z, where Z = i - 1. This involves understanding complex numbers and how to represent them in the complex plane to find their argument.
Answer
$\frac{3\pi}{4}$
Answer for screen readers
$\frac{3\pi}{4}$
Steps to Solve
- Express the complex number in the standard form
Rewrite $Z = i - 1$ in the standard form $Z = a + bi$, where $a$ and $b$ are real numbers. So, $Z = -1 + i$. Here, $a = -1$ and $b = 1$.
- Determine the quadrant of the complex number
The complex number $Z = -1 + i$ has a negative real part ($a = -1$) and a positive imaginary part ($b = 1$). This means it lies in the second quadrant of the complex plane.
- Calculate the reference angle
The reference angle $\alpha$ is given by $\tan^{-1} \left| \frac{b}{a} \right|$. $$ \alpha = \tan^{-1} \left| \frac{1}{-1} \right| = \tan^{-1}(1) = \frac{\pi}{4} $$
- Calculate the argument
Since the complex number is in the second quadrant, the argument $\theta$ is given by $\theta = \pi - \alpha$. $$ \theta = \pi - \frac{\pi}{4} = \frac{3\pi}{4} $$
$\frac{3\pi}{4}$
More Information
The argument of a complex number is the angle between the positive real axis and the line connecting the origin to the complex number in the complex plane. It provides directional information about the complex number.
Tips
A common mistake is to forget to consider the quadrant in which the complex number lies. The arctangent function only gives values in the range $(-\frac{\pi}{2}, \frac{\pi}{2})$, so you need to adjust the angle based on the quadrant. Another mistake is to confuse the real and imaginary parts when determining the quadrant or calculating the reference angle.
AI-generated content may contain errors. Please verify critical information