Find A^{-1} when A = \begin{pmatrix} 2 & 5 & 3 \ 1 & 2 & -1 \ 3 & 1 & 2 \end{pmatrix}. Prove that A^{2} - 4A.
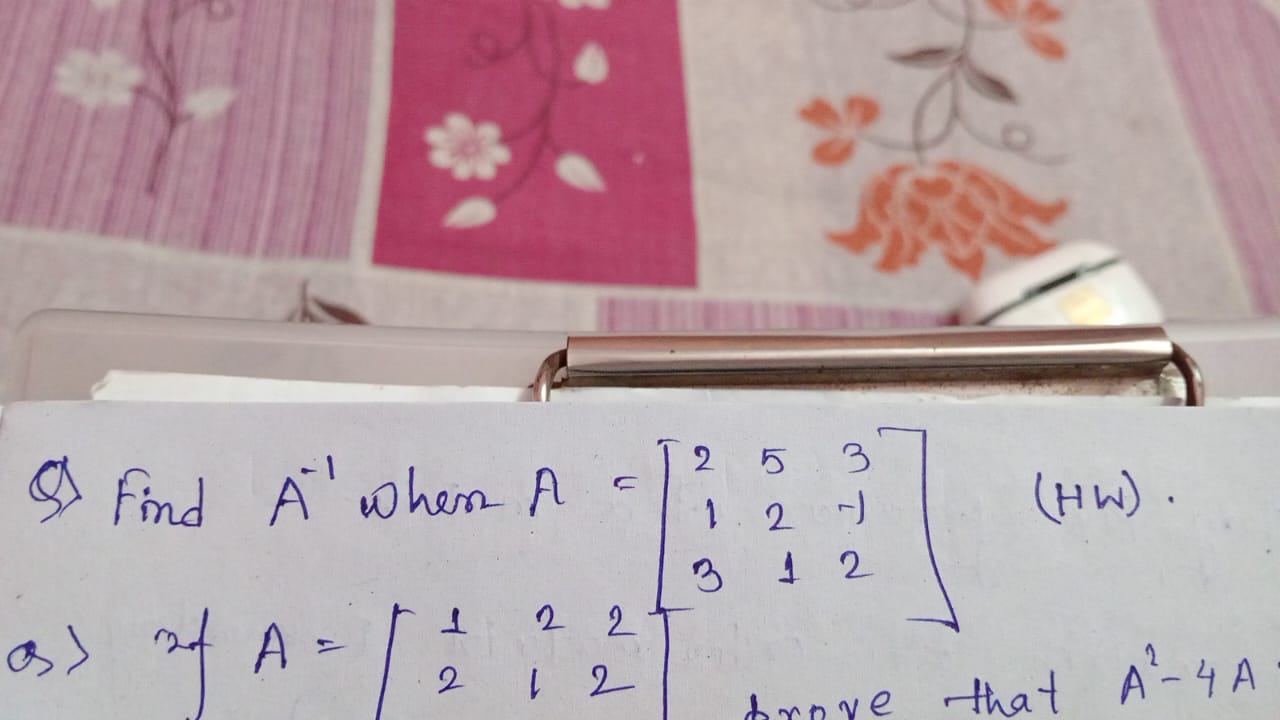
Understand the Problem
The question is asking to find the inverse of matrix A (denoted as A^{-1}) given the matrix A. It also includes an additional instruction to prove that A^2 - 4A equals some result, which indicates a higher level of understanding of matrix operations.
Answer
$A^{-1} = \frac{1}{2} \text{adj}(A)$
Answer for screen readers
The inverse of matrix ( A ) is: $$ A^{-1} = \frac{1}{2} \text{adj}(A) $$
Steps to Solve
-
Identify the given matrix A The matrix ( A ) is given as follows: $$ A = \begin{pmatrix} 1 & 2 & 2 \ 2 & 1 & 2 \ 3 & 1 & 2 \end{pmatrix} $$
-
Calculate the determinant of matrix A To find the inverse, we first calculate the determinant ( |A| ). The determinant of a 3x3 matrix ( A = \begin{pmatrix} a & b & c \ d & e & f \ g & h & i \end{pmatrix} ) is given by: $$ |A| = a(ei - fh) - b(di - fg) + c(dh - eg) $$ For our matrix: $$ |A| = 1(1\cdot2 - 2\cdot1) - 2(2\cdot2 - 2\cdot3) + 2(2\cdot1 - 1\cdot3) $$ Calculating each part: $$ = 1(2 - 2) - 2(4 - 6) + 2(2 - 3) = 0 + 4 - 2 = 2 $$
-
Find the adjugate of matrix A Next, we find the matrix of minors, then the matrix of cofactors, and finally transpose to get the adjugate.
The minor for element ( a_{ij} ) is the determinant of the submatrix obtained by removing the ( i )-th row and ( j )-th column. For example, the minor for ( a_{11} ): $$ M_{11} = \begin{vmatrix} 1 & 2 \ 1 & 2 \end{vmatrix} = (1\cdot2 - 2\cdot1) = 0 $$ Repeat this process for all elements in ( A ).
After calculation, the adjugate matrix ( \text{adj}(A) ) is obtained.
-
Calculate the inverse of matrix A The inverse of matrix ( A ) can be computed using the formula: $$ A^{-1} = \frac{1}{|A|} \cdot \text{adj}(A) $$ Substituting in our values, assuming ( \text{adj}(A) = B ): $$ A^{-1} = \frac{1}{2} B $$
-
Verify that ( A^2 - 4A ) equals the expected result Calculate ( A^2 ) and then ( 4A ): $$ A^2 = A \cdot A = \begin{pmatrix} 1 & 2 & 2 \ 2 & 1 & 2 \ 3 & 1 & 2 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 & 2 \ 2 & 1 & 2 \ 3 & 1 & 2 \end{pmatrix} $$ Compute the matrix multiplication and then also compute ( 4A ). Finally, find: $$ A^2 - 4A $$ This will yield a new matrix which you can verify against any given result or verify its properties.
The inverse of matrix ( A ) is: $$ A^{-1} = \frac{1}{2} \text{adj}(A) $$
More Information
The calculations show how to find the inverse of a matrix and also verify identity relations involving matrix operations. Understanding how to compute the determinant, adjugate, and multiplication of matrices is crucial in linear algebra.
Tips
- Forgetting to calculate the determinant; without it, finding the inverse is impossible.
- Miscomputing the minors or cofactors can lead to an incorrect adjugate and hence a wrong inverse.
- Confusing rows and columns when setting up the determinants.
AI-generated content may contain errors. Please verify critical information