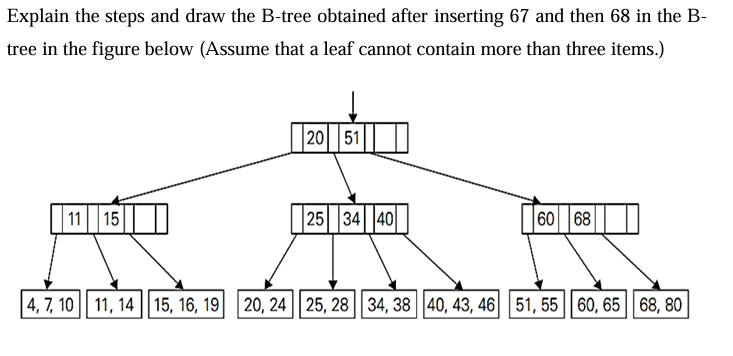
Explain the steps and draw the B-tree obtained after inserting 67 and then 68 in the B-tree in the figure below (Assume that a leaf cannot contain more than three items.)

Steps to Solve

1. Insert 67 into the B-tree

Find the appropriate leaf node for inserting 67. Start at the root:

• Compare 67 with 20 (move right) and then 51 (move right) to the node containing 60 and 68.
• The leaf node before the current leaf node (60, 68) is empty.

Insert 67 into the appropriate place in the node (60, 68):

After insertion:

• Leaf node now contains: 60, 67, 68.

2. Check for Violations in the Leaf Node After First Insertion

The current leaf node (60, 67, 68) adheres to the restriction, as it has only three items.

3. Insert 68 into the B-tree

Again, find the appropriate leaf node for inserting 68. Start at the root:

• Compare 68 with 20 (move right), then 51 (move right) to reach the node containing 60, 67, and 68.

Insert 68 into the same leaf node (60, 67, 68):

After insertion, the leaf node contains: 60, 67, 68, 68.

• Since a leaf can only have a maximum of three items, we need to split this node.

4. Split the Leaf Node

Since the node has four items, split it:

• The middle value (67) becomes the new node.
• Create a new leaf node: one leaf node retains 60, adds 68, and the new node has only 67:
  • Left leaf: 60, 68
  • Right leaf: 68

5. Update Parent Node

After the split, place the new middle value (67) into the parent node (51):

• The parent node (51) now becomes (51, 67).

Now, the B-tree looks like:

        20          51
      /  |        /   \
  11  15  25  34  40  60  67
  / \  / \  /      \
4, 7, 10, 14, 20, 24, ... ,  68

6. Final Adjustments

Lastly, verify that the tree adheres to B-tree properties, ensuring all nodes are balanced and leaf levels consistent.

        20          51
      /  |        /   \
  11  15  25  34  40  60  67
  / \  / \  /      \
4, 7, 10, 14, 20, 24, ... ,  68