Expand (x^2 + 1/x^2)^6
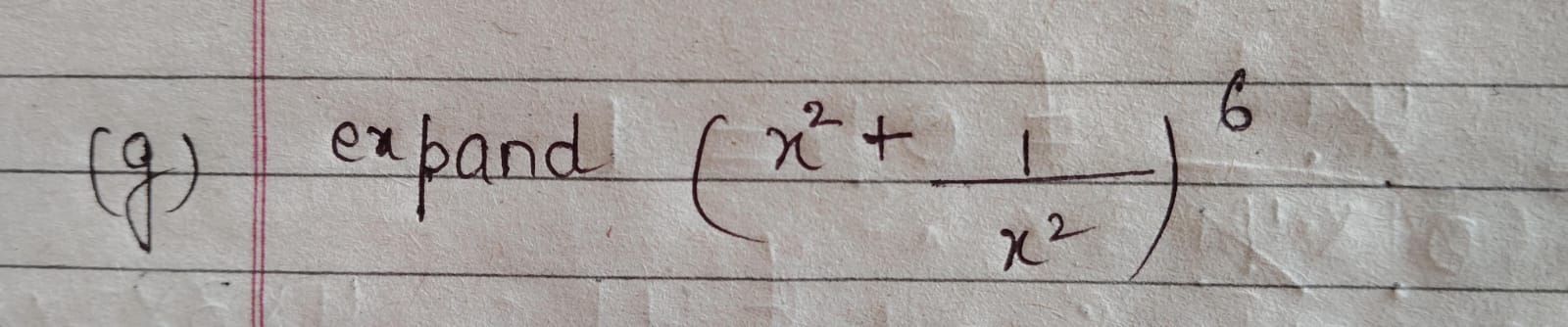
Understand the Problem
The question is asking us to expand the expression (x^2 + (1/x^2))^6, which involves applying the binomial theorem or polynomial expansion techniques to simplify the expression.
Answer
The expansion is: $$x^{12} + 6x^{10} + 15x^8 + 20x^6 + 15x^4 + 6x^2 + 1$$
Answer for screen readers
The expansion of $(x^2 + \frac{1}{x^2})^6$ is: $$x^{12} + 6x^{10} + 15x^8 + 20x^6 + 15x^4 + 6x^2 + 1$$
Steps to Solve
-
Identify the Binomial Expansion Formula
The binomial theorem states that for any positive integer $n$, $$(a + b)^n = \sum_{k=0}^{n} \binom{n}{k} a^{n-k} b^k$$
where $\binom{n}{k}$ is the binomial coefficient. -
Set Variables for the Expansion
Let $a = x^2$ and $b = \frac{1}{x^2}$.
We are expanding $(x^2 + \frac{1}{x^2})^6$, so here $n = 6$. -
Apply the Binomial Theorem
Using the binomial expansion, we write:
$$(x^2 + \frac{1}{x^2})^6 = \sum_{k=0}^{6} \binom{6}{k} (x^2)^{6-k} \left(\frac{1}{x^2}\right)^k$$ -
Simplify Each Term
Each term in the sum is:
$$\binom{6}{k} x^{2(6-k)} \cdot \frac{1}{x^{2k}} = \binom{6}{k} x^{12 - 2k}$$
The expansion becomes:
$$\sum_{k=0}^{6} \binom{6}{k} x^{12 - 2k}$$ -
List Out All Terms
Calculate $\binom{6}{k}$ for $k = 0$ to $6$:
- For $k = 0$: $\binom{6}{0} x^{12 - 0} = 1 \cdot x^{12}$
- For $k = 1$: $\binom{6}{1} x^{12 - 2} = 6 \cdot x^{10}$
- For $k = 2$: $\binom{6}{2} x^{12 - 4} = 15 \cdot x^{8}$
- For $k = 3$: $\binom{6}{3} x^{12 - 6} = 20 \cdot x^{6}$
- For $k = 4$: $\binom{6}{4} x^{12 - 8} = 15 \cdot x^{4}$
- For $k = 5$: $\binom{6}{5} x^{12 - 10} = 6 \cdot x^{2}$
- For $k = 6$: $\binom{6}{6} x^{12 - 12} = 1 \cdot x^{0} = 1$
- Combine All Terms
Now, combine all calculated terms: $$(x^2 + \frac{1}{x^2})^6 = x^{12} + 6x^{10} + 15x^8 + 20x^6 + 15x^4 + 6x^2 + 1$$
The expansion of $(x^2 + \frac{1}{x^2})^6$ is: $$x^{12} + 6x^{10} + 15x^8 + 20x^6 + 15x^4 + 6x^2 + 1$$
More Information
This expansion illustrates how binomial coefficients can reveal the structure of polynomial expressions. The coefficients reflect the number of ways terms can be selected in the expansion.
Tips
- Forgetting to correctly simplify exponents during expansion.
- Not applying the binomial theorem correctly, leading to missing terms.
AI-generated content may contain errors. Please verify critical information